|
Terug naar
de inhoudsopgave BBM
Wiskundige achtergronden bij
de F R A C T A L - o r g a n i s a t i e
© Jules Ruis
Met dank aan prof.dr. J. Molenaar van het IWDE en prof.dr.ir.
J.B.O.S. Martens van ID TU/e
van de Technische Universiteit Eindhoven
Inhoudsopgave
(Bron: 'Chaos, Fractals
& Dynamica' van Robert L. Devaney)
Inleiding
Wat zijn dynamische systemen ?
De begrippen 'functie' en 'iteratie'
De 'baan' van een dynamisch systeem
Iteratie met behulp van de computer
Grafische analyse
De kwadratische familie
Iteratie in het complexe vlak
De Julia-verzameling
De Mandelbrot-verzameling
Geometrische iteratie en fractals
Chaos
Julia-verzamelingen van andere functies
13.1 Polynomen van een hogere graad
13.2 De formule van Euler
13.3 Julia-verzamelingen van transcendente functies
13.4 Explosie van Julia-verzamelingenDe Julius-verzameling
De Julius-verzameling
De 'vulling’ van de Julia-verzamelingen; het ‘Ruis-gebied’
De Julius-Ruis-verzameling
De inverse functies van polynomen
De 3e dimensie van de Julius-Ruis-verzameling
Het computerprogramma BBM.exe
1. Inleiding
Veel mensen denken dat wiskunde een dood vak is;
dat de wiskunde zijn einde vond bij Pythagoras, wiens stelling zich
de meesten van ons nog wel herinneren. Wij hebben er als regel geen
notie van wat de wiskunde in werkelijkheid doet, met welke vraagstukken
het zich bezighoudt en wat de drijfveren zijn voor wiskundigen om
er mee aan de slag te gaan. Het onderwerp 'dynamische systemen' biedt
de gelegenheid de wiskunde in een meer modern daglicht te plaatsen.
Juist vanuit haar klassieke en 'universele' karakter vormt de wiskunde
de basis voor alle andere disciplines. Helaas loopt een aantal vakgebieden
ver achter in het gebruik van de 'moeder van alle wetenschappen'.
Met name de organisatiekunde heeft in het licht van de jongste ontdekkingen
op wiskundig gebied uitdagende mogelijkheden laten liggen.
2. Wat zijn
'dynamische systemen' ?
Naast de studie van systemen in evenwicht ('statische
systemen') onderscheiden we een tak in de wiskunde die zich bezig
houdt met 'dynamische systemen'. Dit zijn in beweging verkerende processen;
processen die in de loop der tijd veranderingen ondergaan. Dynamische
systemen treffen we aan in alle disciplines. De veranderende weersomstandigheden
in de metereologie, de fluctuaties van de populatie-omvang in de ecologie
en de groei van bloemen en planten in de biologie. Ook in de organisatiekunde
van vandaag staan veranderingen centraal, in belangrijke mate in gang
gezet door de dynamiek van de voor een organisatie relevante omgeving.
Ten behoeve van dit vakgebied treft u onderstaand een wiskundige inleiding
aan op het gebied van 'dynamische systemen'.
3. De begrippen
'functie' en iteratie'
Vanuit wiskundige optiek gaat het in een dynamisch
systeem met discrete tijdstappen om het telkens weer (bijvoorbeeld
n keer) toepassen van een wiskundige functie of afbeelding.
Een functie is een operatie (een opdracht, een bewerking) die volgens
een voorgeschreven recept, bij elk getal uit een zekere verzameling
van getallen één bepaald getal produceert. Een bekend
voorbeeld is de 'kwadraat'-functie: T(x)=x² hetgeen
betekent, dat bij elk getal x het product van dat getal met
zichzelf wordt afgeleverd. 'Iteratie' betekent dat dit proces telkens
wordt herhaald, waarbij een verkregen uitkomst (output) weer wordt
gebruikt als input voor de volgende berekening. Het 'iteratie proces
van de kwadraatfunctie in n-stappen', in formule: Tn(x)=x²,
gaat uit van een bepaalde gekozen startwaarde ‘x’ en bestaat
er uit dat de gekozen functie T(x) achtereenvolgens n
maal wordt herhaald. Het iteratie-proces van de kwadraat-functie met
3 iteratiestappen levert voor de startwaarde '2' de tussenuitkomsten
'4' en '16' op en heeft als einduitkomst de waarde '256'. Naast de
'kwadraatfunctie' T(x)=x² en vergelijkbare functies van een
hogere graad, beschouwen we in deze verhandeling ook S(x)=sin x,
C(x)=cos x en E(x)=exp x.
4. De 'baan'
van een dynamisch systeem
De rij van de geïtereerde waarden van een punt/getal
noemen we de baan van dat punt/getal. Zo bestaat de baan van
2 onder de functie T(x)=x² uit de rij van getallen: 2, 4, 16,
256, 65536, etc. Deze rij nadert op de duur 'oneindig'. Dit is het
geval voor alle getallen x, waarvan de absolute waarde groter
is dan 1 (|x|>1). Indien |x|<1 dan nadert de rij
naar 0. Indien x=1 dan geldt dat Tn<(x)=1
voor alle waarden van n. We hebben hier te doen met een vast
punt van T, ook wel dekpunt genoemd.
Het onderzoek naar het gedrag van alle banen van
een gegeven dynamisch systeem noemen we baan-analyse. Nu doet
zich de fundamentele vraag voor: ‘Kunnen wij voor een gegeven dynamisch
systeem voorspellingen doen omtrent het lot van alle banen? Kunnen
wij van te voren vast stellen wat er zal gebeuren bij voortgezette
iteratie.’
Voor een aantal systemen luidt het antwoord bevestigend.
In werkelijkheid kan een dynamisch systeem echter heel veel verschillende
baantypen vertonen. We noemen een aantal van deze baantypen.
- Een belangrijk baantype, zoals in het geval van x² en sin
x, wordt geleverd door een dekpunt. Een dekpunt van F
is een punt xo waarvoor geldt dat F(xo)=xo.
- Een ander type baan is de periodieke baan of cykel
(eigenlijk 'cyclus'). De baan van het punt xo noemen
we periodiek als hij na een aantal iteraties N in
zijn uitgangspunt xo< terugkeert. Het kleinste
positieve getal N waarvoor dat geldt, heet de periode
van de periodieke baan. Het punt xo noemen we
een periodiek punt van periode N. Periodieke banen
of cykels zijn van belang, omdat zij een weerspiegeling zijn van
zich herhalende verschijnselen in de natuur, zoals de met de seizoenen
fluctuerende omvang in populaties van bepaalde soorten insecten.
- Als laatste belangrijke baantype noemen we de banen die uiteindelijk
vast of uiteindelijk periodiek zijn. Deze ontstaan uit
punten die weliswaar niet zelf vast blijven of periodiek zijn, maar
die ergens in hun baan een vast punt of een periodiek punt hebben.
Zo is bijvoorbeeld het punt x=-1 voor de functie T(x)=x²
'uiteindelijk vast', omdat T(-1) ongelijk is –1, zodat
–1 geen vast punt is, doch T(-1)=1 en 1 wèl een vast
punt is. Voor de functie F(x)=x4-1 is het punt
1 'uiteindelijk periodiek' omdat F(1)=0, terwijl 0 een periodiek
punt is van periode 2.
5. Iteratie met behulp van de computer
Het werken met dynamische systemen vergt het maken
van vele berekeningen. Nu hedentendage de personal computer beschikbaar
is, met zijn fantastische snelheid van verwerking, is een gouden tijdperk
voor het gebied van de dynamische systemen in de wiskunde en informatica
aangebroken. Met zeer eenvoudige programma's, geschreven in Powerbasic,
zijn binnen enkele seconden miljoenen berekeningen mogelijk.
6.Grafische analyse
De toegenomen resolutie van beeldschermen en de mogelijkheid
tot presentatie van kleurenplaatjes m.b.v. LCD-projectoren, maakt een
grafische, dus visuele, analyse van de gepresenteerde resultaten van
dynamische systemen mogelijk. De resultaten van meerdere berekeningen
kunnen zichtbaar naast elkaar op het scherm worden geplaatst. Daarbij
wordt gebruik gemaakt van een goede ordening van het beschikbare kleurenpallet.
Bij het afbeelden van wiskundige functies en objecten
worden de x- en y-coördinaten van de functie of het object vertaald
naar vergelijkbare posities op het beeldscherm, dat als regel linksboven
begint met het beeldschermpunt (0,0). We kunnen echter heel gemakkelijk
het relevante deel van het beeldscherm (en daarmee de grootte van het
object) verkleinen. In de door ons gebruikte computerprogramma's gaan
we als volgt te werk. We berekenen binnen het relevante deel van het
beeldscherm voor elk beeldschermpunt (x,y) de waarde van de functie
of het object. Daarbij geven we tevens de criteria aan waaronder dat
punt moet worden 'opgelicht' en zo ja, in welke kleur dat oplichten
moet gebeuren.
7. De kwadratische familie
De familie van kwadratische functies, Qc(x)=x²+c,
waar c een reële parameter is, vertoont een uiterst gecompliceerd
dynamisch gedrag. We hebben hier te doen met een simpele niet-lineaire
functie (d.w.z. niet van de vorm ax+b). We zoeken op de eerste
plaats die c-waarden, waarvoor de dynamica van Qc(x)
interessante eigenschappen vertoont. M.a.w. we zoeken voor elke c-waarde
de verzameling van xo-waarden, waarvan de Qc-baan
niet naar oneindig wegtrekt. Dit blijkt het geval te zijn voor c<=¼.
Alle banen van Qc voor c>¼ trekken weg naar
oneindig. Als c afneemt langs c=¼ zien we hoe een paar
dekpunten 'geboren wordt'. Hier zien we een voorbeeld van bifurcatie.
Bifurcatie betekent een 'splitsing in tweeën', een 'wijziging',
een 'vertakking'. In het gegeven voorbeeld zien we dat Qc
voor het eerst een dekpunt heeft als c=¼, en dat er plotseling
bij kleiner wordende waarden van c een splitsing in twee dekpunten
verschijnt. Dit is een voorbeeld van wat bekend staat onder de naam
zadelknoop-bifurcatie.
8. Iteratie in het complexe vlak
We kunnen de functie Qc ook toepassen
op complexe getallen en voor de parameter c een complex getal
kiezen. De iteratie van een functie van een complexe variabele behoort
ongetwijfeld tot een van de meest fascinerende onderwerpen van de dynamica.
Het complexe getal i voldoet aan de betrekking i²=-1.
Er bestaat uiteraard geen reëel getal dat aan deze voorwaarde voldoet.
Een complex getal ziet eruit als z=x+iy, waar x en y
reële getallen zijn. Het getal x heet het reële
deel van het complexe getal z en het getal y draagt
de naam imaginaire deel van z. Complexe getallen hebben
een geometrische interpretatie. Een complex getal kan immers in het
vlak worden afgebeeld als het punt (x,y). Elk punt van het vlak
kan dus worden gezien als een complex getal. Het getal i komt
daarbij terecht in het punt (0,1). De modulus | x+iy
| van het complexe getal x+iy is per definitie de afstand van
het punt (x,y) tot de oorsprong. Met complexe getallen kunnen
algebraïsche bewerkingen worden uitgevoerd. Bijv. z² = x² -
y² + i(2xy) en ez = ex (cos y + i sin y)
In het dynamisch gedrag van de complexe kwadraatfunctie
overheersen twee soorten van gedrag: punten met modulus kleiner dan
1 itereren naar het dekpunt 0; punten met modulus groter dan 1 itereren
naar oneindig. Dan resteren nog de punten waarvan de modulus precies
gelijk is aan 1. Die punten vullen de 'eenheidscirkel' van het complexe
vlak op. De verzameling van die punten vormt de zogenaamde Julia-verzameling
van de functie T(z)=z².
9. DeJulia-verzameling
Rond 1918 ontdekte de Franse wiskundige Gaston Julia
(1893-1978) vele eigenschappen van de verzameling die thans zijn naam
draagt. Voor een polynoom-functie luidt de nauwkeurige definitie van
zijn Julia-verzameling aldus: het is de rand van de verzameling der
punten waarvan de baan wegtrekt naar oneindig. In het kader van deze
inleiding zijn vooral de geometrische eigenschappen van de Julia-verzameling
interessant. In figuur 9 treft u een voorbeeld van een Julia-verzameling
aan van Qc(z)= z²+c voor de waarde c=-0,75.
Zoals reeds eerder opgemerkt, is het eigenlijk de rand, of de grens,
van de getekende plaatjes die de naam Julia-verzameling draagt. De volledig
gekleurde verzameling wordt aangeduid met de naam opgevulde Julia-verzameling,
of uitgebreide Julia-verzameling. We zullen tijdens het toenemen
van de c-parameter tot 0,25 aldaar een 'implosie' te zien krijgen van
de opgevulde Julia-verzameling. Tijdens het passeren van dit bifurcatiepunt
desintegreert de Julia-verzameling tot fractaal stof, een structuur
die formeel de naam Cantor-verzameling draagt. Dit verschijnsel
vindt bij het passeren van de Julia-grens (van binnen naar buiten) op
elke plek plaats. Bij het afnemen van c vindt bij het passeren
van het punt c=-0,75 een periodeverdubbelings-bifurcatie plaats.

Fig. 9. Julia-verzameling voor
c=-0,75
10. De Mandelbrot-verzameling
Het dynamisch gedrag van de kwadratische functie Qc(z)=z²+c
(met c als complexe parameter) kan voor verschillende waarden
van c sterk uiteenlopen. Ook bij de Julia-verzamelingen (J)
van de Qc's is er voor verschillende waarden van c
een grote variatie van vormen te zien. Het was de wiskundige Benoit
Mandelbrot die ontdekte dat de naar hem genoemde Mandelbrot-verzameling
(M) een soort 'catalogus' verschaft van al deze uiteenlopende
structuren (M vormt een soort parameter-bassin voor J).
We leggen er de nadruk op dat de Mandelbrot-verzameling een deelverzameling
is in het c-vlak en dus niet ligt in het z-vlak waar de
Julia-verzamelingen hun leven doorbrengen.
De Mandelbrot-verzameling is betrekkelijk eenvoudig
te construeren, ondanks zijn gecompliceerde aard. Hiertoe bekijken we
de baan van 0 onder Qc voor elke waarde van de parameter
c. Omdat deze baan zo'n speciale, kritische rol vervult in het
duiden van de dynamica, staat deze bekend als kritische baan,
terwijl het punt 0 de naam kritisch punt draagt. Hoewel het dus
voor de hand ligt te zoeken naar die c-waarden, waarvoor de kritische
baan niet naar oneindig trekt, werd de vraag pas in 1978 door Mandelbrot
gesteld (en beantwoord). Als een van de eersten vroeg hij naar de gedaante
van de verzameling van c-waarden met niet naar oneindig wegtrekkende
kritische baan. Zijn vondst is wel eens aangemerkt als 'het meest ingewikkelde
object uit de gehele wiskunde'. Het wordt ook wel het 'Appelmannetje
van Mandelbrot' genoemd. In figuur 10 treft u de Mandelbrot-verzameling
aan.

Fig. 10. De Mandelbrot-verzameling
De verzameling M bestaat uit een dominerend
hartvormig gebied, waaraan verscheidene 'versieringen' zijn vastgehecht.
De spitse punt van het hartvormige gebied bevindt zich precies in het
punt c=¼, het punt waar de zadelknoop-bifurcatie optreedt. Direct
links van het hartvormige gebied bevindt zich een groot cirkelvormig
gebied. Deze 'bobbel' is aangehecht bij het punt c=-¾, het punt
van de periodeverdubbelings-bifurcatie. Tenslotte is er nog een 'staart'
of 'antenne' te zien, die naar links wijst. Die staart ligt op de reële
as en eindigt precies bij c=-2, de parameterwaarde waarvoor oneindig
veel periodieke punten kunnen worden aangewezen.
Bij het nader inzoomen van bepaalde gebieden van M
verschijnen kleine kopieën van M. In de 'baby'-Mandelbrot
verzamelingen treffen we dezelfde structuur aan als in de 'moeder'-verzameling.
De M-verzameling is een samenhangende verzameling. De ogenschijnlijk
losse 'eilandjes' die in de omgeving van het hoofdgebied zijn te zien,
zijn in werkelijkheid verbonden door dunne sprietige draadjes, die in
de gebruikte resoluties helaas niet zichtbaar zijn.
11. Geometrische
iteratie en fractals
In de wiskunde zijn er veel processen die geïtereerd
kunnen worden. We hebben gezien hoe de iteratie van een functie verloopt.
De iteratie van bepaalde geometrische constructies produceren de gecompliceerde
objecten die met de term 'fractal' worden aangeduid. Mandelbrot kwam
tot het inzicht dat de vreemde, schijnbaar gekunstelde constructies
die eerdere wiskundigen hadden geschapen, in het geheel niet zo pathologisch
waren als men eerst dacht. Hij toonde het tegendeel aan door te laten
zien dat allerlei natuurobjecten zoals kustlijnen, wolken, bladeren
en bergketens door fractals te beschrijven zijn. De gewone geometrische
constructies met rechte lijnen en gladde krommen en oppervlakten waren
ontoereikend om de ingewikkelde patronen uit de natuur te begrijpen
en te beschrijven.
Wat is eigenlijk een fractal? Men kan zeggen dat
een fractal een geometrische vorm is, een object dus, met een gebroken
(fractale) dimensie. Het object is bovendien veelal gelijkvormig;
het levert bij herhaalde vergroting steeds weer hetzelfde beeld op.
Daarbij kunnen we onderscheiden:
- zelf-similaire fractals; geconstrueerd door een constructieregel
herhaald toe te passen. Voorbeelden hiervan zijn de 'zeef van Sierpinski'
(een gelijkzijdige driehoek, waaruit we al itererend de middelste
driehoek verwijderen) en de 'kromme van Koch' (onstaat door een
oneindige reeks van toevoegingen aan de rand van een gelijkzijdige
driehoek).
- niet zelf-similaire fractals; bij inzoomen krijgen we steeds hetzelfde
patroon te zien, maar het is niet exact een kopie van het gehele
object. De Julia-verzameling en Mandelbrot-verzameling zijn hiervan
voorbeelden.
Rest de vraag hoe we aan een geometrisch object een
dimensie toekennen. De dimensies van een lijnstuk, een vierkant en
een kubus zijn respectievelijk 1, 2 en 3. Voor meer ingewikkelde constructies
gebruiken we een meer formele benadering. Daarbij delen we een object
op in stukken, elk met een afmeting gelijk aan het n-de deel
van de afmeting van het oorspronkelijke object. Hoeveel stukken hebben
we dan nodig om het oorspronkelijke object samen te stellen? In de
gegeven voorbeelden respectievelijk n¹, n² en n³
stukken. We definiëren de dimensie D nu als volgt: D=log(aantal
stukken)/log(vergrotingsfactor). Voor de zeef van Sierpinski
geldt: D=log3/log2=1.585…; jawel, een dimensie die ongelijk
is aan een geheel getal. Dit noemen we een gebroken dimensie.
12. Chaos
Het begrip 'chaos' is een van de belangrijkste nieuwe
thema's in de wiskunde. In feite worden we omringd door chaos. De warrelende
patronen die een wervelstorm op het radarscherm van de metereoloog teweegbrengt,
de draaikolken en het geruis van een bergstroom, de fluctuaties in de
aandelenmarkt, de grillige patronen van opstijgende rookwolken; het
zijn allemaal verschijnselen die zich schijnen te onttrekken aan orde
en voorspelbaarheid. Al deze fenomenen zijn van nature chaotisch. De
wezenlijke doorbraak die de wiskundigen recentelijk tot stand brachten,
baseert zich op het inzicht dat chaotische systemen niet noodzakelijk
van een groot aantal variabelen moeten afhangen, maar dat zelfs één
enkele variabele al chaos kan produceren. Een zeer essentieel kenmerk
van chaotische systemen is de gevoelige afhankelijkheid van de beginwaarden.
('Een kuchje in Peking kan een storm in New York veroorzaken').
De complexe kwadraatfunctie T(z)=z² is een goed
voorbeeld van een chaotische functie. Natuurlijk zijn niet alle banen
van de kwadraatfunctie onvoorspelbaar. Wij zagen al dat de baan van
z voor |z|<1 getrokken wordt naar het aantrekkende
dekpunt 0. Als |z|>1, dan trekt de baan van z
naar oneindig. De overige punten liggen op de eenheidscirkel |z|=1.
Deze eenheidscirkel valt precies samen met de Julia-verzameling van
T.
13. Julia-verzamelingen van andere functies
De in voorgaande paragrafen aan de orde gekomen familie
van kwadratische functies is de eenvoudigste groep van niet-lineaire
functies. Er zijn evenwel vele andere functie-families waarin de besproken
verschijnselen en andere interessante fenomenen zich voordoen.
13.1 Polynomen
van hogere graad
Elk polynoom heeft een Julia-verzameling, maar ter
wille van de eenvoud zullen we ons beperken tot de speciale polynomen
van de vorm Pn,c(z)=zn+c, waar n=3,
4, 5, 6….. De exponent n heet de graad van de polynoom.
Omdat de polynomen Pn,c een enkele kritische baan
hebben, bestaat er voor elke n een analogon van de Mandelbrot-verzameling.
Net als bij de kwadratische familie bestaat dit analogon uit alle c-waarden
waarvoor de kritische baan van Pn,c (n>2) niet
naar oneindig wegtrekt. Die verzameling valt weer precies samen met
de verzameling c-waarden waarvoor de Julia-verzameling van P2,c
samenhangend is. De aldus verkregen verzameling draagt de naam bifurcatie-verzameling
van graad n (het eerder genoemde parameter-bassin).
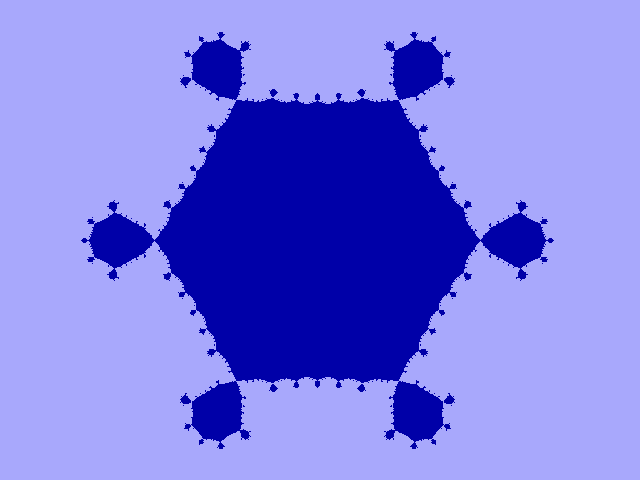
In de figuren 13-A1 t/m 13-D1 treft u de bifurcatie-verzamelingen
aan van de graad 3, 4, 5 en 6. In de figuren 13-A2 t/m 13-D2 treft u
de Julia-verzamelingen aan voor de polynomen met de overeenkomstige
graad. De verschillende c-waarden hiervan liggen in het gebied -2<c<-.7
De verzamelingen voor n=2 werden reeds afgebeeld
in de figuren 9 en 10.
| 
|
|

|
|
Fig. 13-A1. Bif.-verz. van graad 3 |
|
Fig. 13-A2. Julia-verz. voor z graad 3 |
| 
|
|

|
|
Fig. 13-B1. Bif.-verz. van graad 4 |
|
Fig. 13-B2. Julia-verz. voor z graad 4 |
| 
|
|

|
|
Fig. 13-C1. Bif.-verz. van graad 5 |
|
Fig. 13-C2. Julia-verz. voor z graad 5 |
| 
|
|
|
|
Fig. 13-D1. Bif.-verz. van graad 6 |
|
Fig. 13-D2. Julia-verz. voor z graad 6 |
13.2 De
formule van Euler
De formule van Euler legt een verband tussen de exponentionele
functie en de trigonometrische functies sin x en cos x.
De gebruikelijke exponentionele functie wordt geschreven als ex
of exp x, waar e het grondtal is van de natuurlijke logaritme.
Het getal e is bij benadering gelijk aan 2.71828…. De exponentionele
functie komt veelvuldig voor in de wiskunde en ook in andere wetenschappen,
waar hij opduikt in processen als populatiegroei, samengestelde interest
en radioactief verval. De formule van Euler stelt ons in staat om een
complex analogon te vinden van exp x, sin x en cos
x.
De formule van Euler luidt: eix = cos
x + i sin x
Kiezen wij in de formule van Euler voor x de
waarde pi , dan resulteert de volgende verrassende gelijkheid: ei.pi
= cos pi+ i.sin pi = –1
M.b.v. de formule van Euler kunnen we de e-macht
van een complex getal vinden:
ez = e(x+iy) = ex
(cos y + i sin y)
13.3 Julia-verzamelingen
van transcendente functies
Functies zoals de exponentiële functie, de sinus
en de cosinus worden transcendente functies genoemd. Voor transcendente
functies concentreren wij ons op de verzameling van punten waarvan de
baan naar oneindig wegtrekt. In figuur 13-E1 treft u de bifurcatie-verzameling
van de exponentionele functie aan. In figuur 13-E2 is een Julia-verzameling
van Ec(z) = c.ez afgebeeld.
| 
|
|

|
|
Fig. 13-E1. Bif.-verz. exp.functie |
|
Fig. 13-E2. Julia-verzameling van c.ez |
Met behulp van de formule van Euler kunnen we de complexe
sinus en de complexe cosinus introduceren.
sin z = (eiz – e–iz)/2 en
cos z = (eiz + e–iz)/2
In figuur 13-F1 en figuur 13-G1 treft u de bifurcatie-verzamelingen
van de sinus en de cosinus aan. In figuur 13-F2 en figuur 13-G2 zijn
de Julia-verzamelingen van sin z en cos z afgebeeld.
| 
|
|

|
|
Fig. 13-F1. Bif.-verzameling sinus |
|
Fig. 13-F2. Julia-verz. van sin z |
| 
|
|

|
|
Fig. 13-G1. Bif.-verz. cosinus |
|
Fig. 13-G2. Julia-verz. van cos z |
13.4
Explosie van Julia-verzamelingen
We hebben gezien dat Julia-verzamelingen van polynoom-functies
soms dramatische veranderingen ondergaan, namelijk bij een zadelknoop-bifurcatie
en een periodeverdubbelings-bifurcatie. Soortgelijke gebeurtenissen
vinden ook plaats bij transcendente functies. De spectaculaire bifurcaties
zoals we die bij de complexe exponentiële functie, de complexe
sinus en de complexe cosinus tegenkomen, duiden we aan met de term explosie.
Dit gedrag in de complexe dynamica werd voor het eerst waargenomen in
het midden van de jaren tachtig. Zo ondergaat de Julia-verzameling van
cez een dramatische wijziging vanaf circa c=1/e
= 0.36788.
In figuur 13-H is deze explosie vanaf x=0,4 in 25
stappen van 0,001 weergegeven.
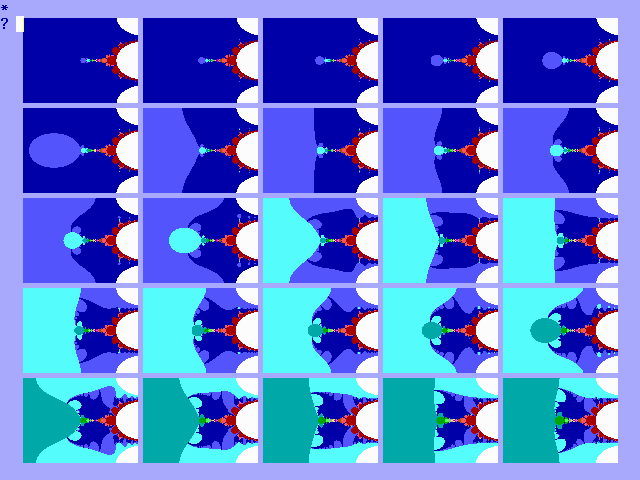
Fig. 13-H. Explosie van cez
vanaf x=.4 in 25 stappen van 0,001.
Ook in de familie c sin z en c cos z
treden soortgelijke verschijnselen op bij het passeren van de grenzen
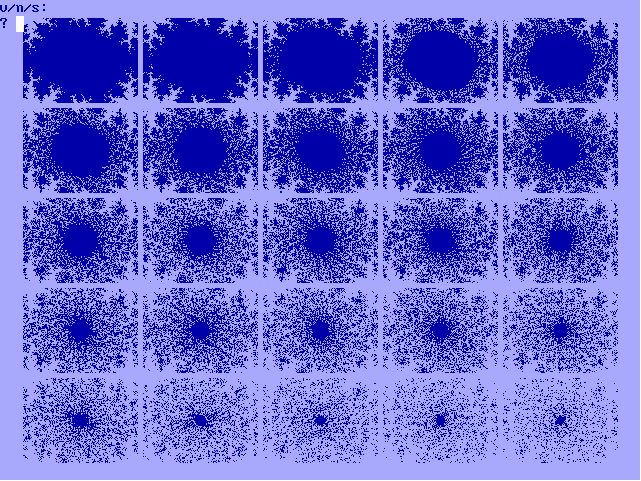
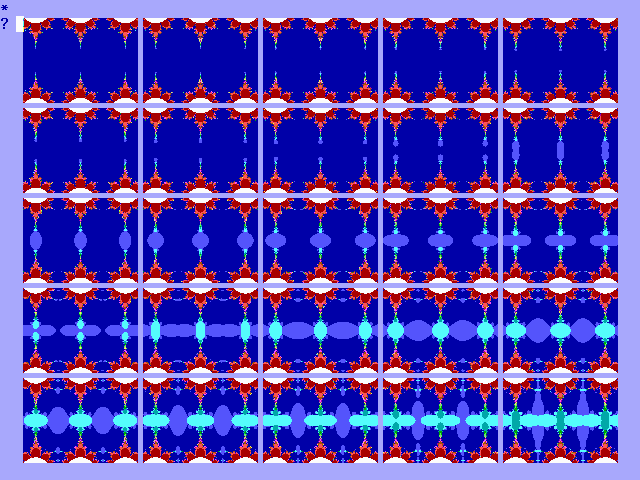
van de bifurcatieverzameling. In figuur 13-I is de explosie van (0.6+0.8i)
sin z in een reeks van 25 afbeeldingen weergegeven. In figuur 13-J
zijn voor 0,7i cos z met 25 stappen van y=0.001
de veranderingen afgebeeld.
| 
|
|
|
|
Fig. 13-I. Explosie van (0.6+0.8i) sin
z |
|
Fig.13-J Explosie van 0.7i cos z |
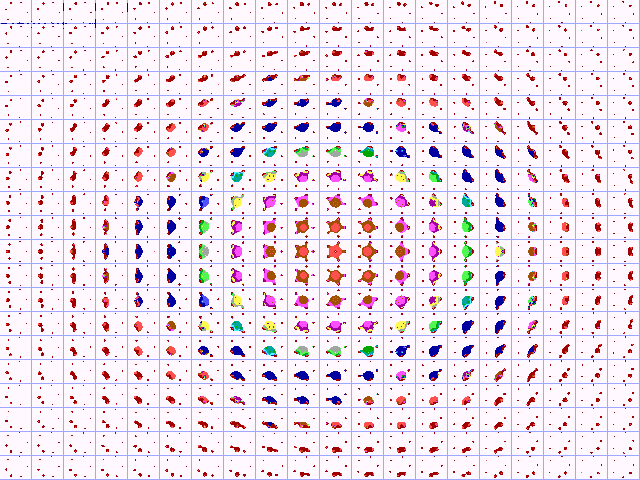
14. De Julius-verzameling
In bovenstaande beschouwing hebben we (met uitzondering
van figuur 13-H) steeds één enkele Julia-verzameling afgebeeld.
Met een meer iteratief gebruik van het specifiek voor dit doel ontworpen
computerprogramma is het mogelijk meerdere ‘plaatjes’ tegelijk op het
scherm te vertonen. Daarbij houden we op het scherm in principe de x/y-grenzen
aan, met x = Re(c) en y = Im(c), waarbinnen
een bepaalde functie nog een Julia-verzameling vertoont. Dit zijn dus
de grenscoördinaten van de bifurcatie-verzameling. We beelden voor
een systematische reeks van beeldschermpunten de Julia-verzamelingen
in verkleinde vorm af op het scherm, bijvoorbeeld in een aantal van
20 x 20 = 400 plaatjes. Het resultaat is een totaal-patroon, dat overeenkomt
met de bifurcatie-verzameling van de desbetreffende functie. Deze meta-verzameling
van Julia-verzamelingen noemen we, refererend aan de voornaam van de
schrijver van dit artikel, de 'Julius-verzameling'. Wiskundig
heet dit het direct product van twee ruimten. In figuur 14 treft u de
Julius-verzameling aan voor de polynoom z²+c.

Fig. 14. De Julius-verzameling
voor z²+c
De afgebeelde Julius-verzameling loopt van –1.5<Re(c)<0.5
en van –1<Im(c)<1
15. De
'vulling' van de Julia-verzamelingen; het Ruis-gebied
Zoals eerder aangegeven wordt de Julia-verzameling
gedefinieerd als de grens tussen banen die wegtrekken naar oneindig
en banen die itereren naar 0. Het gebied van alle banen die convergeren
naar 0 definieerden we als de opgevulde Julia-verzameling. Thans definiëren
we het gebied van alle banen die wegtrekken naar oneindig als de uitgevulde
Julia-verzameling. Het betreffende gebied noemen we het Ruis-gebied.
Gegeven een bepaald complex getal c=a+ib onderzoeken we voor
elk beeldschermpunt B in een aantal iteratie-stappen het gedrag van
de baan van het betreffende getal c. Daarbij gelden de volgende
uitgangspunten.
We definiëren een relatief klein getal e
, met 0<e <1, en een relatief
groot getal t , met t
>1. Noemen we de afstand tussen twee opeenvolgende iteratie-beelden
'd' dan geldt:
d=(x-x1)(x-x1) + (y-y1)(y-y1). We zeggen nu
dat het betreffende beeldschermpunt een element is van de opgevulde
Julia-verzameling indien c.q. zodra d<e
.
We zeggen dat het beelschermpunt een element is
van de uitgevulde Julia-verzameling indien c.q. zodra d>t
De k-de stap waarbij voor de eerste keer
aan de e /t
-voorwaarde wordt voldaan noemen we het vluchtgetal K.
Aan elk vluchtgetal koppelen we een bepaalde kleur van het pixel dat
moet worden opgelicht. Daarmee ontstaan op het scherm samenhangende
kleurpatronen met eenzelfde vluchtgetal. Door de waarden van de getallen
e en t te variëren
ontstaan verschillende structuren.
In de literatuur wordt aan de afgebeelde kleurpatronen
nauwelijks aandacht besteed. Nader onderzoek hiervan levert verbluffende
resultaten op. De samenhang in de kleurpatronen die aanwezig blijkt
tussen opeenvolgende Julia-plaatjes, maakt het geheel tot een film van
metaforische groei. In figuur 15 treft u een voorbeeld aan van een Julia-verzameling,
die zowel is opgevuld als uitgevuld. Hierin is waar te nemen dat het
kleurenpatroon, vertrekkend vanuit de rand van de Julia-verzameling,
naar binnen en naar buiten in eenzelfde volgorde verloopt.

Fig. 15. De Julia-Ruis-verzameling,
zowel opgevuld als uitgevuld, van z²+c voor c=-,75
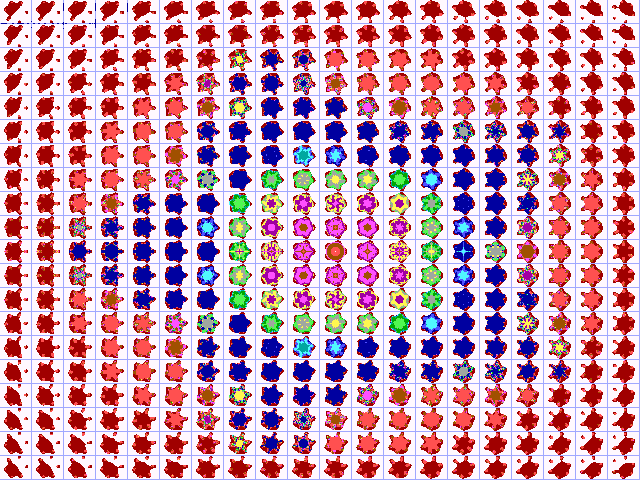
16. De
Julius-Ruis-verzameling
Het is met een kleine wijziging in het computerprogramma ook mogelijk
de Julius-ver-zameling ‘uitgevuld’ af te beelden. Deze uitgevulde Julius-verzameling
noemen we de Julius-Ruis-verzameling. In figuur 16A treft u deze verzameling
aan voor z²+c.

Fig. 16A. De Julius-Ruis-verzameling
voor z²+c
Duidelijk is te zien dat de Julius-verzameling gelijkenis
vertoont met de Mandelbrot-verzameling. Bovendien is helder waar te
nemen, dat de afbeeldingen in de omgeving van de Julius-verzameling
(waarvan we eerder dachten dat de Julia-verzameling overging in fractaal
stof, om vervolgens geheel te verdwijnen) ook een fractal-structuur
bezitten.
Meerdere Julius-Ruis-verzamelingen
In figuur 16-B t/m 16-J zijn de Julius-Ruis-verzamelingen
afgebeeld voor de eerder in deze notitie behandelde functies. Bij elke
JR-verzameling is tevens de bijbehorende bifurcatie-verzameling opgenomen,
echter thans voorzien van een uitgevuld Ruis-gebied.
Voor de volledigheid zijn ook de functies van graad
1 opgenomen. Dit zijn lineaire afbeeldingen. Derhalve worden 'slechts'
cirkels getoond.
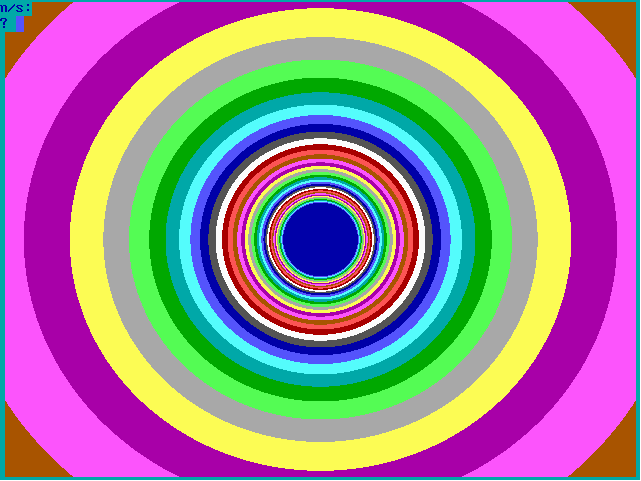
| 
|
|
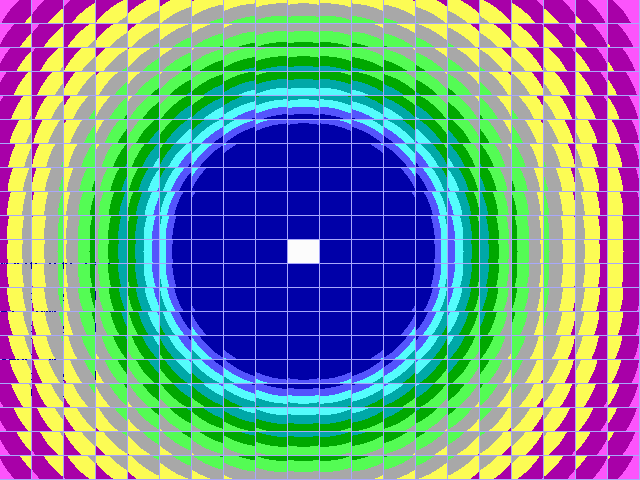
|
|
Fig. 16-B1. Bif.-Ruis-verz. van graad 1 |
|
Fig. 16-B2. JR-verzameling voor z graad 1 |
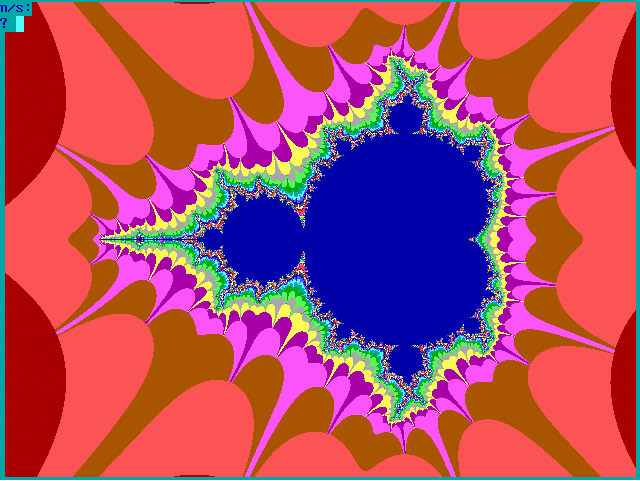
| 
|
|

|
|
Fig. 16-C1. Bif.Ruis-verz. van graad 2 |
|
Fig. 16-C2. JR-verzameling voor z graad 2 |
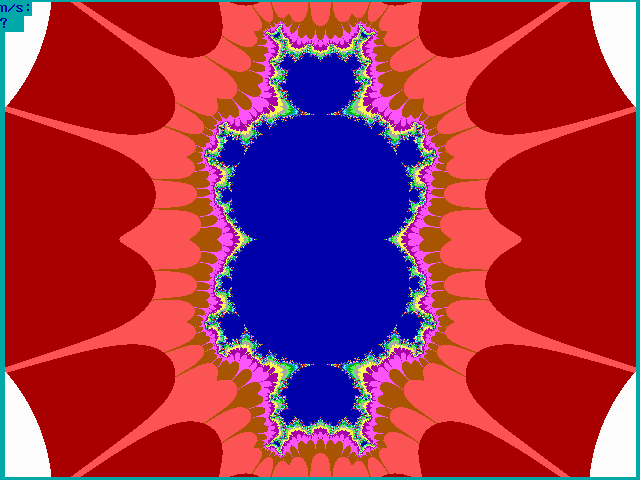
| 
|
|
|
|
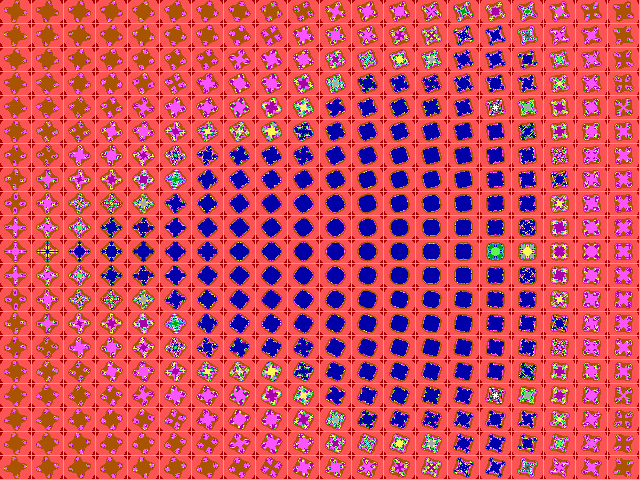
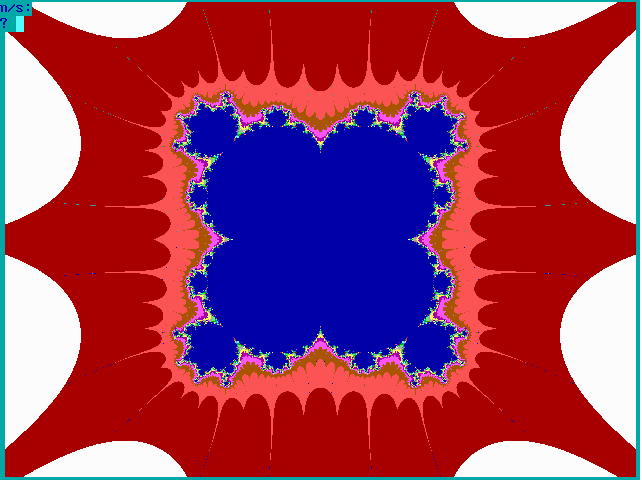
Fig. 16-D1. Bif.Ruis-verz. van graad 3 |
|
Fig. 16-D2. JR-verzameling voor z graad 3 |
| 
|
|
|
|
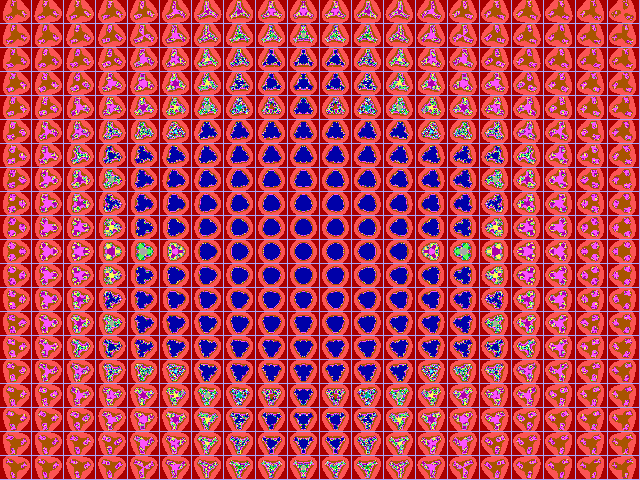
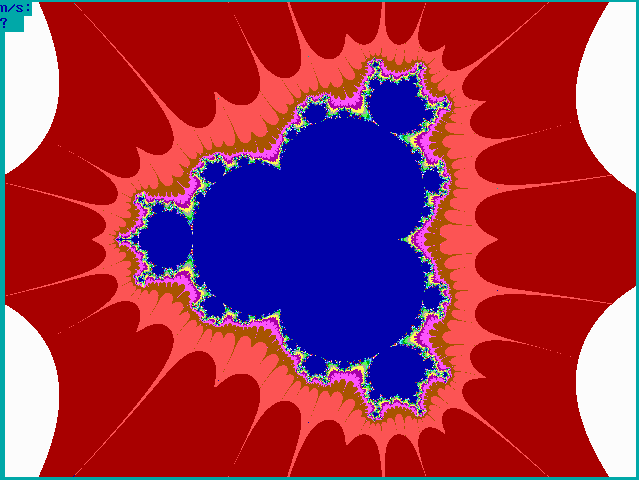
Fig. 16-E1. Bif.Ruis-verz. van graad 4 |
|
Fig. 16-E2. JR-verzameling voor z graad 4 |
| 
|
|
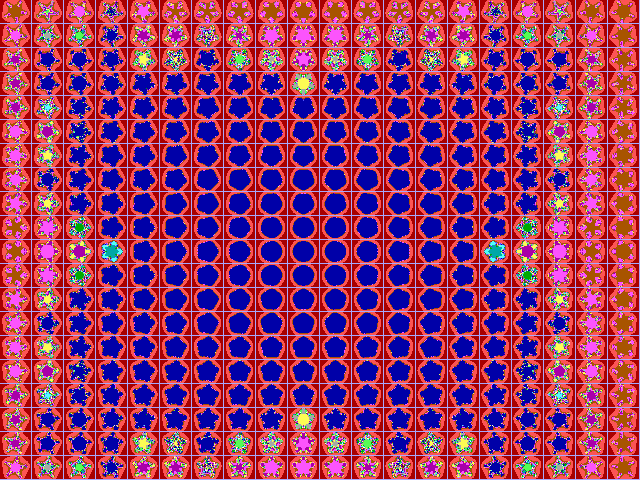
|
|
Fig. 16-F1. Bif.Ruis-verz. van graad 5 |
|
Fig. 16-F2. JR-verzameling voor z graad 5 |
| 
|
|
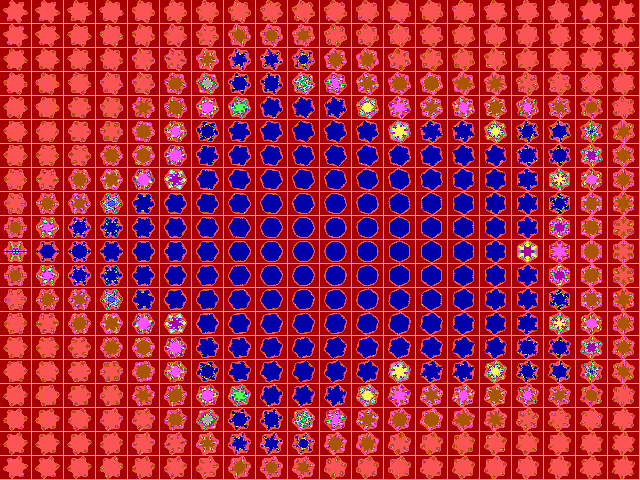
|
|
Fig. 16-G1. Bif.Ruis-verz. van graad 6 |
|
Fig. 16-G2. JR-verzameling voor z graad 6 |
| 
|
|

|
|
Fig. 16-H1. Bif.Ruis-verz. van sinus |
|
Fig. 16-H2. JR-verzameling voor sinus z |
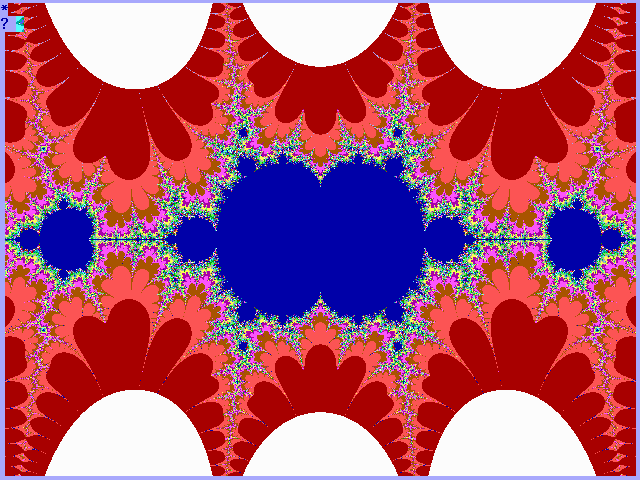
| 
|
|
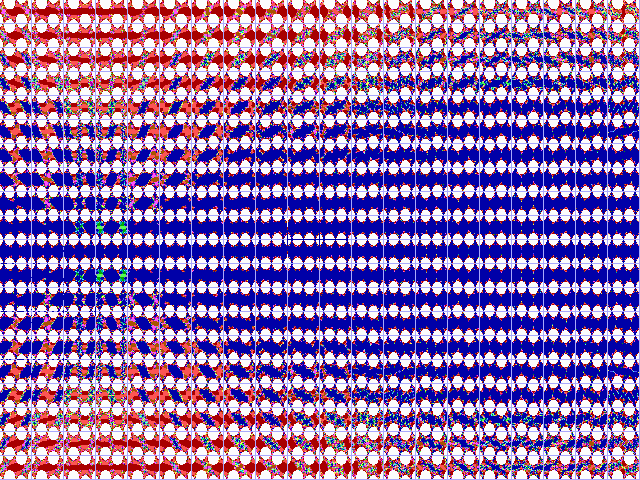
|
|
Fig. 16-I1. Bif.Ruis-verz. van cosinus |
|
Fig. 16-I2. JR-verzameling voor cosinus z |
| 
|
|
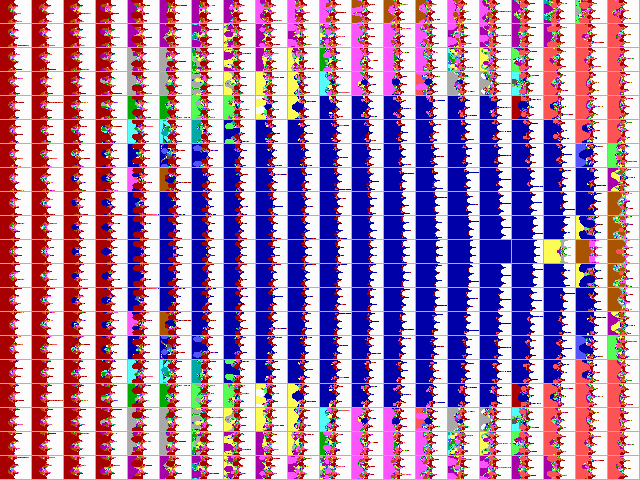
|
|
Fig. 16-J1. Bif.Ruis-verz. voor exp. |
|
Fig. 16-J2. JR-verzameling voor exp. z |
17. De inverse functies van polynomen
Elk polynoom heeft een Julius Ruis verzameling. In
het voorgaande hebben wij ons beperkt tot speciale polynomen van de
vorm Pn,c(z)=zn+c, waar n=3, 4,
5, 6….. De exponent n noemden we de graad van de polynoom.
Met behulp van de polaire representatie van een polynoom kunnen we de
speciale gevallen veralgemeniseren. Daarvoor schrijven we het complexe
getal z=a+i.b als z=r.ei.fi, waarbij a=r.cos
fi en b=r.sin fi; fi = arctan (b/a). Dan geldt vervolgens: zn+c=(rn.cos(n.fi)+a)
+ i.( rn.sin(n.fi)+b).
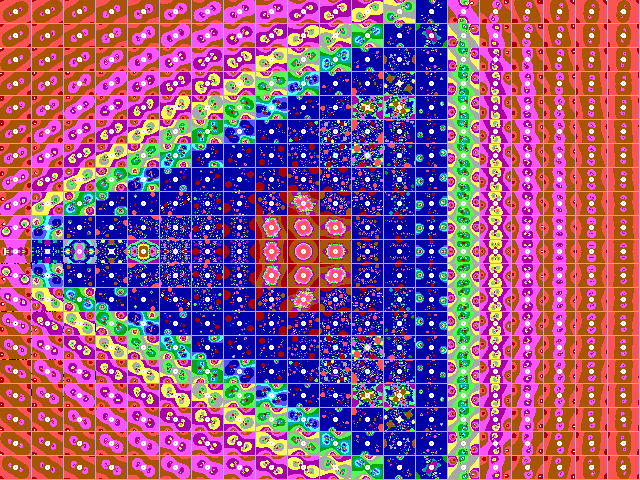
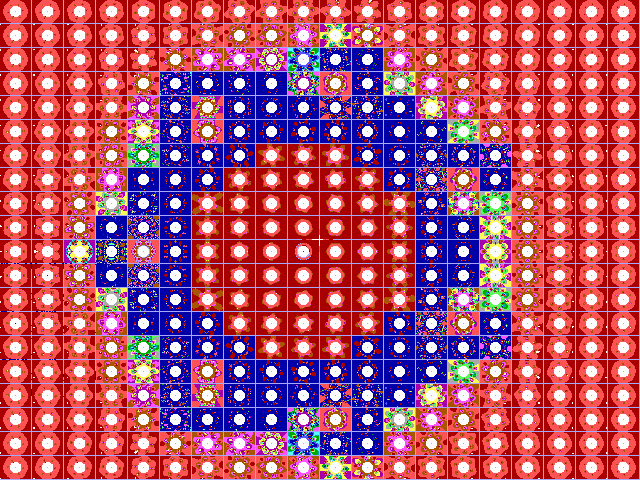
In figuur 17-A en 17-B treft u de Julius-Ruis-verzameling
aan voor respectievelijk de polynomen z-2
en z-6 . Figuur 17-C bevat de Julia-Ruis-verzameling
van c.z-6 voor c=i maal 1.2
| 
|
|
|
|
Fig. 17-A. JR-verzameling voor z graad -2. |
|
Fig. 17-B. JR-verzameling voor z graad -6. |

Figuur 17-C. Julia Ruis verzameling c.z-6<
voor c=i maal 1.2
18. De 3e dimensie van de Julius-Ruis-verzameling
De waarde van e , in combinatie
met het getal K (het aantal iteraties), bepaalt voor een bepaald complex
getal c=a+ib de structuur en de kleur van de opgevulde Julia-verzameling.
Naarmate de absolute waarden van a en b afnemen, dient
uiteraard een steeds kleinere waarde voor e
te worden genomen om met succes (= kleurrijke scherpe inwendige structuur)
te voldoen aan de waarde d<e .
Bij het naderen van a,b=0,0 nadert e
naar 0. Hierbij dient te worden opgemerkt dat de gebruikte computer
zelfs bij mutaties van e kleiner dan 15 cijfers
achter de komma (doorlopend tot zelfs het door de gebruikte computer
bepaald minimum van 45 cijfers achter de komma) structuurwijzigingen
te zien geeft. Dit verschijnsel hangt mogelijk samen met de opslagcapaciteit
van een 32-bits computer en verdient nader onderzoek vanuit de optiek
van het analyseren van fouten.
De waarde van t , in combinatie
met het getal K (het aantal iteraties), bepaalt voor een bepaalde
c de structuur en kleur van het externe Ruis-gebied. Bij een kleine
waarde van t (bijvoorbeeld t
=1) wordt bij de eerste iteratie reeds voldaan aan de voorwaarde
d>t . Het vluchtgetal K
is dan derhalve 1 (in het gebruikte kleurenpallet de kleur ‘wit’). Bij
groter wordende t vult de Ruis-ruimte zich
met meerdere kleuren; de Ruis-ruimte dijdt dan als het ware uit. Bij
het verder toenemen van t (tot het door de
gebruikte computer bepaald maximum van 38 cijfers voor de komma) lossen
de buitenkleuren als het ware weer geleidelijk aan op.
Met het introduceren van e
en t is aan de JR-verzameling (naast x
en y) een 3e dimensie toegevoegd.
Vele combinaties van 'groeiende' e
en t zijn mogelijk. In figuur 18-A 1 t/m
4 treft u enkele voorbeelden aan van drie-dimensionale groei van z6
+ c waarbij genoemde grootheden sprongsgewijs toenemen.(e
groeit van 1 naar 10 tot de macht -45 en springt vervolgens naar 0,
en t groeit van 1 naar 10 tot de macht +38,
zijnde de grenzen van de gebruikte computer).
Fig. 18-A1/2/3/4 De groeiende
3e dimensie van de Julius-Ruis-verzameling
Het is interessant de a/b-coördinaten van het
Ruis-gebied van de Julius-Ruis-verzameling verder uit te breiden. In
figuur 18-B zijn de a/b-coördinaten van de plaatjes in figuur 18-A
met een factor 5 vermenigvuldigd. Deze uitbreiding laat zien dat de
binnenste gebieden van de JR-afbeelding het beeld blijven vertonen van
de bifurcatie-verzameling. De buitenkant tendeert echter bij groter
wordende a,b naar een cirkel. De precieze vorm verdient echter
nog nader onderzoek.
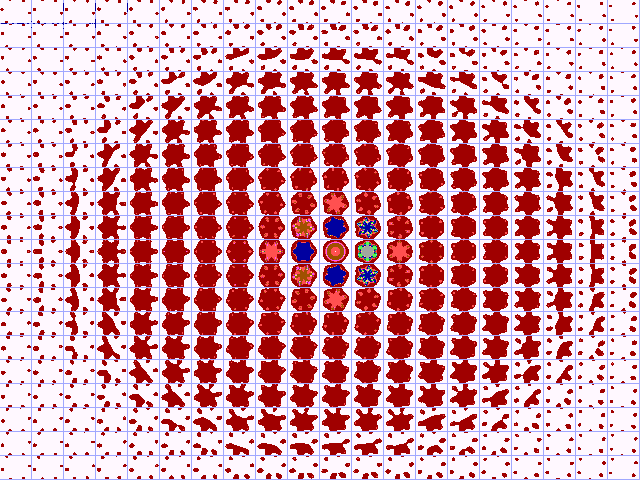
Fig. 18-B. De Julius-Ruis-verzameling
van z6+c (5x vergroot)
19. Het computer-programma
BBM.exe
De parameters voor het genereren van Julia/Julius-Ruis-verzamelingen
zijn opgenomen in een computerprogramma BBM.exe, waarmee op systematische
wijze bovengenoemde fractallen kunnen worden afgebeeld. BBM staat voor
Bewustzijns Besturings Model.
De Julius-verzamelingen van de diverse functies bestrijken
(met uitzondering van de exponentionele functie) in het BBM.exe hetzelfde
gebied. Dit gebied is de basis voor een genormeerd BBM, het Norm Bewustzijns
Besturings Model. De functies zijn hierin genormeerd op 20 eenheden
op elke as. De gebieden zijn:
Polynomen: -2 < x < 2 en -1.5 < y
< 1.5
Sin/cos-functie: -2 < x < 2 en -1.5 <
y < 1.5
Exponent. functie: -4 < x < 1 en -3 <
y < 3
Het BBM.exe bestaat uit drie hoofdprogramma's:
- Programma voor het afbeelden van de bifurcatie-(Ruis)-verzamelingen
(Mandelt.exe)
- Programma voor het afbeelden van Julia-(Ruis)-verzamelingen.
- Programma voor het afbeelden van Julius-(Ruis)-verzamelingen.
De volgende variabelen kunnen in elke combinatie naar
de wens van de gebruiker worden gekozen.
- Naam van de gebruiker.
- Bifurcatie-verzameling (y/n)
- Soort object: polynoom graad n=1 t/m 8, of sin, cos of exp.
- In genormeerde vorm of niet (norm heet BBM).
- Afbeelden met/zonder beeldinformatie/tekst (alleen bij beeld 1).
- Alleen opgevulde of ook uitgevulde Ruis-verzameling (heet 'omgeving').
- Aantal 'beeldjes' op scherm (400, 25, 9, 3 in 1, of 1).
- Vergrotingsfactor (VF) buitenwereld (bij BBM met omgeving).
- Itereren van x, y of x/y gelijktijdig.
- Grootte van de x/y iteratie stappen.
- Itereren van max. aantal stappen n (max. K) en daarmee kleur-iteratie.
- Grootte iteratie-stappen K.
- Itereren van getal e (kleinste ondergrens)
en daarmee de inwendige structuur (niet van invloed op sin, cos en
exp.).
- Grootte iteratie-stappen e .
- Itereren van getal t (grens voor buitenwereld)
en daarmee de uitwendige structuur (alleen in combinatie met ‘omgeving’).
- Beeldschermgebied N itereren (grootte van het plaatje).
- Grootte iteratie-stappen N.
- Startwaarde A (x); in BBM: A
- Startwaarde B (y); in BBM: B
- Startwaarde K; in BBM: C
- Startwaarde e (P1); in BBM: D1
- Startwaarde t (P2); in BBM: D2
- Startwaarde N; in BBM: E
De afgebeelde plaatjes kunnen met de combinatie-toetsen
Alt/PrtSc op het clipboard van de computer worden geplaatst. Met het
programma MsPaint kunnen deze plaatjes als bestand worden opgeslagen,
worden geprint of in andere programma’s worden geladen (MS Word of Powerpoint).
In figuur 19-A wordt de output van het genormeerde
BBM getoond. De in het plaatje afgebeelde tekst geeft bovengenoemde
startwaarden weer. In de kop van het plaatje wordt het genoemde kleurenpallet
getoond (K-waarden 1 t/m 15).
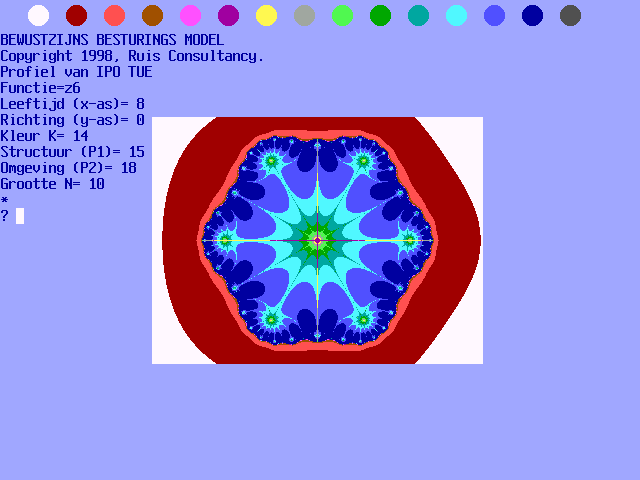
Fig. 19-A. Het genormeerde
Bewustzijns Besturings Model (BBM), met kleurenpallet.
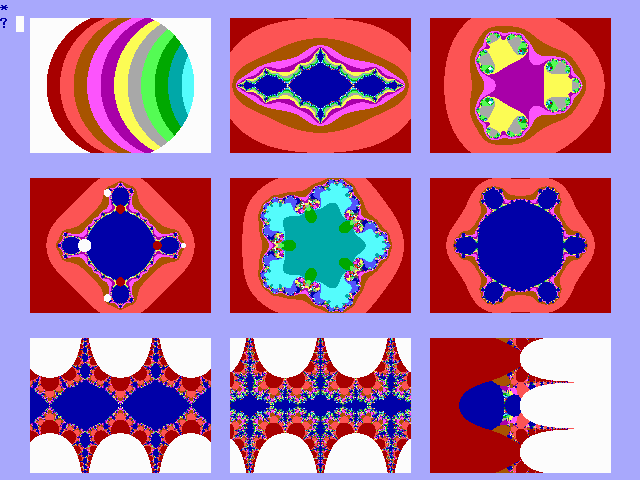
Op de startpagina van dit rapport zijn de negen
besproken functies conform het genormeerde BBM bijeen geplaatst. De
variabelen zijn: A=4, B=0, C=13, D1=19, D2=10 en E=4.
De exp.functie vertoont langs de y-as een repeterend
beeld met een cyclus van 2p . In figuur 19-B1
wordt de schitterende afbeelding getoond van de functie p
.i.ez.
De exp.functie kent ook een aantal explosies. In
figuur 19-B2 is een typische exponentionele explosie weergegeven.
De figuren 19-C1 en 19-C2 tonen de Julia-verzameling
van z²+c voor c=0,25 respectievelijk zonder en met het
zogenaamde Ruis-gebied.

Fig. 19-B1. De functie van p
.i.ez
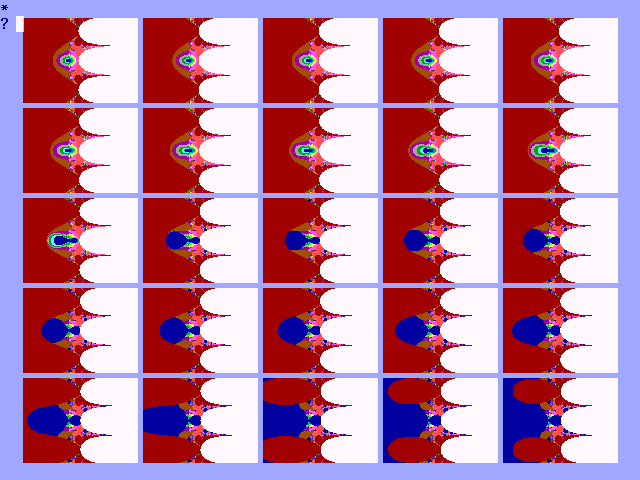
Fig. 19-B2. Explosie van de
exponentionele functie in het punt (-4, 0)

Fig. 19-C1. De Julia-verzameling van z²+c
voor c=0,25 zónder het zogenaamde Ruis-gebied

Fig. 19-C2. De Julia-verzameling
van z²+c voor c=0,25 mét het zogenaamde Ruis-gebied
De ware fractal-liefhebber kan zelf aan het experimenteren met het
programma BBM.exe. Click daarvoor op de toets 'Ga naar computerprogramma
BBM.exe'. U treft daar een nadere instructie aan.
|