Return to index Life Sciences Publications

Spatial Neural Networks Based on Fractal Algorithms
Biomorph Nets of Nets of ...

1 . Abstract and Introduction :
Biological central nervous systems with their massive parallel structures and recurrent projections show fractal characteristics in structural and functional parameters ( Babloyantz and Louren¸o 1994 ). Julia sets and the Mandelbrot set are the well known classical fractals with all their harmony , deterministic chaos and beauty , generated by iterated non - linear functions .The according algorithms may be transposed , based on their geometrical interpretation , directly into the massive parallel structure of neural networks working on recurrent projections. Structural organization and functional properties of those networks , their ability to process data and correspondences to biological neural networks will be discussed .

2. Fractal algorithms and their geometrical interpretation :
2.1 The algorithms of Julia sets and the Mandelbrot set:
Iterating the function f(1) : z (n+1) = c + zn2 ,(c and z representing complex numbers respective points in the complex plane), will generate the beautiful fractals of the Julia sets and the Mandelbrot set (Mandelbrot 1982 , Peitgen and Richter 1986) . According to the rules of geometrical addition and multiplication of complex numbers ( Pieper 1985) we can interpret function f(1) as describing a combined movement :
First , the term :" + zn2 " in f(1) describes a movement from point zn to the point zn2 . A lot of trajectories can connect these two points, one is the segment of the logarithmic spiral through zn . ( In a polar coordinate system we get a logarithmic spiral by the function f(2): r = aec*j . Geometrical squaring of a complex number is done by doubling the angle between the vector z ( from zero to the point z ) and the x - axis and squaring the length of vector z (2) . Doubling the angle j in f(2) will also cause a squaring of r . This proves point z2 lying on the logarithmic spiral through z .)
Second , the first term of f(1), " c " ( meaning the addition of complex number c ), can be interpreted as describing a linear movement along vector c .
Both movements can be combined to a continuous movement along spiralic trajectories ( according to Poincaré )from any point zn to the according point (c+zn2 ) = z(n+1).We get two different fields of trajectories , one with segments of logarithmic spirals arising from each point z n, the other as a field of (parallel) vectors c .We can follow the different trajectories alternately ( fig 2.1c ) or simultaneously ( fig 2.1d , 2.1e) . Various options to
visualize the developments are shown in figure ( 2.1 a-f ) .

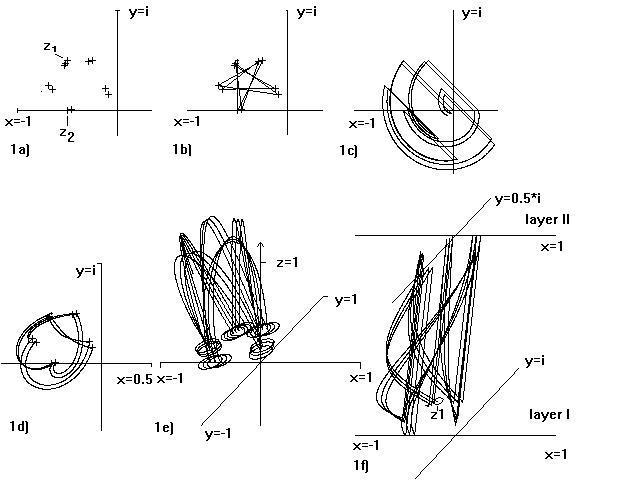
Figure 2.1 : Development of values acc. f ( 1 ) - ( c = -0.5 + 0.5* i , z1 = -0.5+0.5*i;
10 iterations): a) isolated values after each iteration ; b) subsequent values connected ; c) following the trajectories of terms " +c " and " z 2 " alternately ; d ) Trajectories of the combined movement acc. f(1); e ) trajectories acc. Poincaré in 3 - dim. parameter - space, ( intersecting points with complex plane marked by circles ); f) The trajectories projecting from layer I to layer II ( representing term " z 2 " and from layer II to layer I ( acc. term " + c ").

2.2 Three - dimensional algorithms :
We may transfer the principles of function f(1) into spatial algorithms in a three-dimensional coordinate system . Because squaring of a triple of numbers ( coordinates on x - , y - and z - axis ) is not defined , the direct " translation " of f(1) into a three-dimensional algorithm is impossible . The following two algorithms will transfer some of the fundamental functional properties of Julia sets to according three-dimensional fractal structures :
Algorithm I ) In a three-dimensional coordinate system with x -, y - and z-axis we can lay a plane through each point z(x1,y1,z1) and the x-axis.
In this oblique " complex plane" we square z n . To the point " z (x1,y,z1)2 ", which we thus find, we can easily add a three-dimensional vector c(x,y,z).This addition of the constant vector c will bring us to a point z(x2,y2,z2) , which will be the starting point of the next iteration . This algorithm generates interesting spatial fractal structures on the basis of the two - dimensional Julia sets which are formed by the respective vector c.
Algorithm II ) Before adding the vector c in algorithm I , we rotate the oblique "complex plane" together with the point "z (x1,y,z1)2 " around the x - axis , until ist angle with the y-axis of the three-dimensional coordinate system will be doubled . After addition of vector c the next iteration may be started . If we combine all these three partial movements ( along the logarithmic spiral in the oblique "complex plane" from z(x1,y1,z1) to "z(x1,y1,z1)2 " , the rotation of this complex plane around its x-axis and the straight movement along the three - dimensional vector c ) to one movement we get three - dimensional trajectories from every point z(x1,y1,z1) to the according point z(x2,y2,z2) and on this base spatial sets corresponding to two - dimensional Julia sets .

3.1 Neural networks based on fractal algorithms :
In principle all trajectories can be interpreted as symbolic representations of neurons . An iteration of a fractal algorithm will move us from z n to z (n+1). As well , a neuron at any point z n in a network could send its activity along its axon ( following the respective trajectory ) to the point z (n+1) of the neural network . By this we can transpose the fields of trajectories of any analytic function into the structure of a neural network .
The inclusion - criterium of Julia sets ( points belong to the Julia set , if the values we get in the following course of iterations will not leave a defined zone around zero ) can be applied to the neural net too : Neurons will belong to the net ( will survive ) , if they can activate a certain number of neurons in a defined zone around zero .

3.2 Two - dimensional networks :
We can construct neural networks with one or two layers of neurons on the basis of function f(1):
A one - layer - net we get , if the neurons send their axons from the points (zn) directly to the points (c + zn2) = z (n+1) in the same layer ( according fig.1e ).
If we transpose the two terms of function f (1) into two different neural layers, we will get a two-layer network ( according fig. 2.1f and fig. 3.2 )

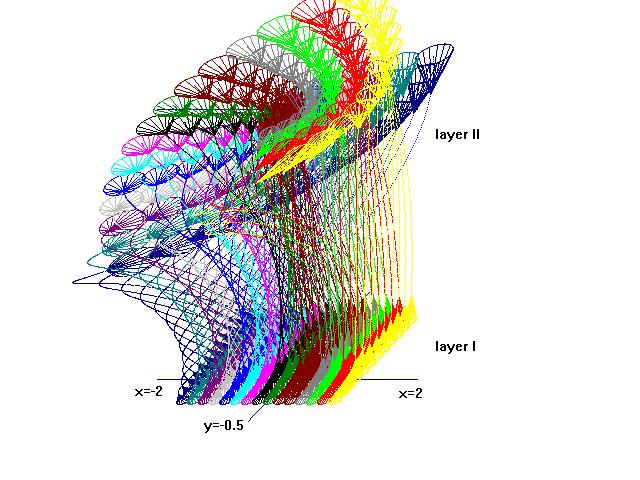
Figure 3.2 : Layer I of a neural network with two neural layers . The axons of the neurons reflect the term " z 2 " of function f(1) .

3.3 Three-dimensional neural networks :
As in the two - dimensional case we interpret trajectories of three-dimen-sional algorithms as functional neurons . Applying the inclusion - criterium of Julia sets , we finally get three - dimensional neural networks ( fig. 3.3 ).

4 . Structural and functional properties and features:
4.1 " Julia " - a network - language?:
Because these networks are based on fractal algorithms ( which they perfectly perform ), the patterns of activations in these networks show all properties of Julia sets like self - similarity and symmetry of generated structures and patterns, occurence of strange attractors , periodic and aperiodic orbits , Siegel discs , zones of con- and divergence, implementation of binary trees and amplification of small differences between slightly different starting patterns.
Activating a neuron at any point zn will cause a sequence of activation of neurons which will reflect the development of the values we get by iterations of function f(1) in geometrical interpretation. In many cases the activation of
two different neurons will lead to an activation of the same circumscribed region in the course of the iterated activations . In this region neurons get

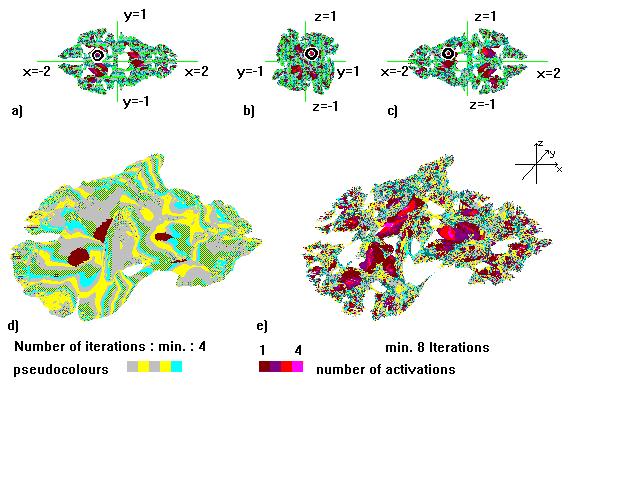
Figure 3.3 : Aspect of a three - dimensional analogon of Julia sets , produced according algorithm II , constant vector c = -0.7(x) + 0.2(y) + 0.4(z) . A)-c) : view of structure e , orthogonal to the indicated plane , d and e) 3-D impression , in d all neurons shown with at least 4 iterations before values leave a radius of 5 around zero , in e) with at least 8 iterations . Light colours are used to show the spatial structure , red colours to indicate neurons , which may activate in the sequence of activation neurons in the region around the point p = -0.4(x) - 0.4(y) - 0.2(z) with radius 0.09 ( region marked in a-c by circle ) directly or by interneurons.

activation from both starting neurons . They will be activated in a higher degree than other neurons . These more activated neurons will be able to indicate the pattern of the simultaneous activity of these two starting neurons ( figure 4.1 ) and may work as " detector - neurons " of the specific input pattern .
4.2 Implementation of binary trees , dialectic network - structure:
According to function f (1 ) , a neuron z as well as its negation , the neuron (-z) will activate the neuron (c + z2 ) . Every neuron will have two predecessor - neurons and one subsequent neuron . The neurons and their connections will perfectly model the structure of a manifold binary tree . This will enable those networks to represent data with hierarchical , binary order very well ( fig. 4.2 ). It should be very suitable for dialectic processes , each neuron z representing the thesis , its negation ( - z ) the antithesis , both

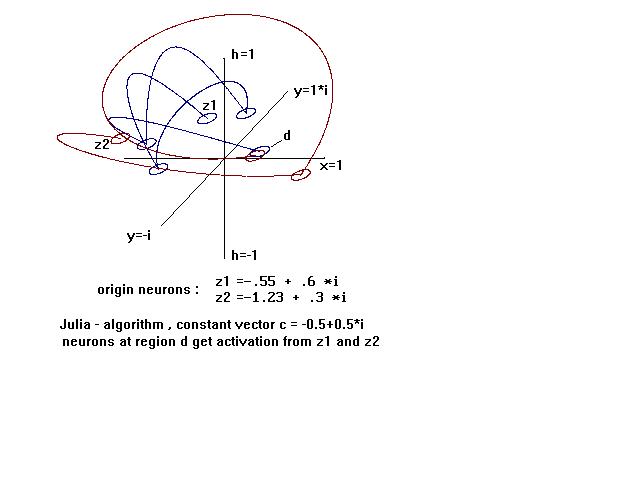
Figure 4.1 :Options for ( if connections are recurrent ) connecting and synchronizing neurons over a great distance and detecting a specific input pattern by increased activation of neurons at d ,which will be activated by both starting neurons z1 and z2 .

projecting their activity to the neuron ( c + z 2 ) as representative of synthesis.
In three- dimensional networks , based on algorithm II ( 2.2 ) , we get instead of a binary tree a quartenary structure with each neuron having four predecessor - neurons , thus increasing the connectivity of the network .

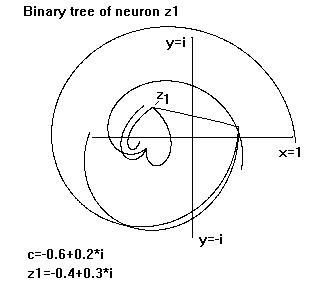
Figure 4.2 : Binary tree of the neuron z1 with two " generations " of predecessor - neurons , one subsequent neuron .
Combining excitatory and inhibitory neurons , the binary structure will allow to represent logical structures in the networks.

4.3 " Somatotopic " structure , synaptic learning , neural columns :
The structure of such networks is massive parallel with neural axons
preserving their relationship during their course , so the neural projections will be " somatotopic "( neighboured neurons will activate neighboured regions of the network )( fig.3.2) .
Each region will receive activation from many other neurons , due to the overlapping structures of axonal endings and due to effects of convergence in fractal functions .Many neurons will compete for activation with their overlapping arboreal dendrites. There will be effects of synaptic learning , varying the pathway of activation , which will be no longer determined only by geometrical algorithmic rules ( as it will be at the very beginning ) , but also by learning - history . Because every signal will have to pass on every transmission a small neural network ( formed by all neurons reaching the area of transmission with their dendritic structures ) , the whole net is working as net of nets of ... . ( In mammalian brains the neural columns may represent these units of neural networks ) .

4.4 Handling of intermediate values :
Fractal functions need a "continuum" of infinitely many numbers , whereas neural nets consist of a limited quantity of neurons .Quite often an activation will not hit only one neuron exactly, but will lead to an activation - maximum between two distinct neurons . Such an intermediate result can be correctly represented by a simultaneous activity of these two neurons analogue to the degree of activation they receive from their predecessor - neurons . This transforming of intermediate values into analogue degrees of activity of the neighboured neurons could be done by the overlapping structures of dendritic and axonal endings . Using these processes , the maximum resolution of two stimuli will no longer depend on the distance between two neurons , but on the distance between two synaptic contacts. By the almost infinite number of synaptic endings in neural networks we get the " Quasi-continuum" of units , fractal processes need . This may be an important task of the arboreal structures of dendritic and axonal endings beyond their role in processes of synaptic learning .

4.5 Amplification of slight differences between input patterns :
Slight differences between two starting patterns may be amplified not only by effects of learning in the individual history of the network but also because of the great sensibility of fractal structures to little changes of starting or intermediate parameters . Similar sensibility to slightly different patterns we can find in biological networks in form of hyperacuity.


4.6 Input and output :
All neurons , or only neurons in specialised regions of the networks , may have connections to peripheral receptors or effectors or they themselves may represent these organs . Thus the network can communicate with the external world .

4.7 Recurrent connections :
In biological nervous systems we often find recurrent projections , each neuron not only activating its subsequent neuron but also the neurons by which it has been activated itself. Such networks will not only perform one algorithm but simultaneously its reversed function , ( in case of function f(1) the function f(3) z ( n+1 ) = ( z (n ) - c ) 1/2 ). In this case all neurons will send their activity to three others ( In case of nets based on algorithm II to five other neurons because of the fourfold symmetry of these structures ). Depending on the algorithm determining the net and the chosen parameters , all neurons may thereby be connected over a smaller or greater distance with almost each other neurons . The activity of one neuron may spread like a wave over the entire net .

4.8 Synchronization of distant neurons , representing complex concepts:
Depending on the choice of the parameter c in function f (1) the course of activation through the neural network follows certain regularities . For instance , the activation will rotate around a fixed point steadily approaching to it , if the point is an attractor , while in case of Siegel discs the activation will rotate in an elliptical orbit around the fixed point (Peitgen and Richter 1986). In case of recurrent connections such networks could work as " phone centers" which may provide a plenitude of possibilities to connect different neurons of the network by " active axonal lines " using the functional properties of fractal structures .These possibilities to connect neurons by only few interneurons as shown in figure 4.1 may allow neurons , being activated by the same object , to synchronize their activity . Synchronous activity seems to be an important feature for representation of objects or complex concepts in central nervous systems . If one starting neuron in fig. ( 4.1 ) should represent the term " cup " , the other the term " tea " , the whole chain of active neurons in fig. ( 4.1 ) may represent the term " cup of tea " .

4.9 Dynamic temporal activation patterns :
Continuous flow of sensoric perceptions will lead to specific temporal activation patterns . In the case of neural networks working with the Julia - algorithm each neuron z 1 has certain subsequent neurons z n . For example , different temporal sequence of activation of 3 origin neurons ( "t1" , "e1" , "n1" ) will produce different clusters of active neurons ( in the group of their subsequent neurons ) . At any iteration ( n ) , " ten " would be represented by simultaneous activity of the neurons t n , e (n-1), n (n-2) , whereas the word " net " would be represented by simultaneous activity of the neurons n n , e (n-1) , t (n-2) . Synaptic learning leading to different limit cycles will enable the net to differentiate between the words .

4.10 Information processing as task of the whole network :
Functional behaviours stem from altered activities of large ensembles of neurons and thus they are a network property ( Wu et al 1994 ). In fractal networks each neuron is influenced by many others and itself influencing also many other neurons . Fig. 4.10a shows an example to which degree a region can be influenced by the entire network . In reversal this region is influencing by recurrent projections wide parts of the net .
The superposition of all wave functions caused by the input neurons will result in an entire wave function . We get an information - coding related to holographic information storage ( The relation becoming even closer , if we assume periodic " coherent " waves of activity, we find in brain functions ( Destexhe 1994 ), interfering with the activity waves caused by the fractal pathways ).

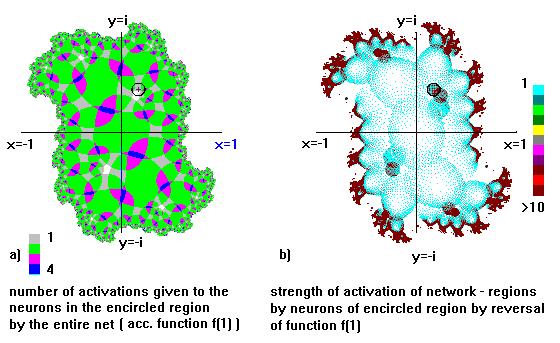
Figure 4.10 : Neural net based on a Julia - algorithm , constant vector c = 0.25 + 0.25*i . A) Indicated by pseudocolours is the degree , to which the network regions can activate neurons in a region around z = 0.17 + 0.43*i with radius 0.065 ( marked by a black circle ) in the course of activation sequences . B) Showing to which degree the neurons of the mentioned circumscribed region can activate other regions of the net by recurrent connections ( reversal of function f(1) according function f(3)).

Each input pattern will cause a highly specific activation pattern as result of the interference of the influences of each input neuron to the whole net . Regarding Fig. 4.10b we can interpret the diagram of the strength of influence of one region or neuron to the net as diagram of some sort of a wave function .

4.11 Options for associative memory functions :
Following considerations may be hypothetical : Activation patterns caused by neural input or active network neurons will cause a specific temporal activation sequence in each neuron . Each neuron may registrate the received activating sequence , for instance in form of ribonucleic-acid -( RNA ) molecules , each ribonucleic nucleotid representing a certain degree of activation ( Corresponding to an old Quechuan knot - script used in Inca - empire ) . The neurons would thereby get filled with lots of such memory - RNA - molecules ( The role of RNA and subsequently produced proteins in learning processes is not yet completely understood ( Birbaumer and Schmidt , 1996)). If there would be no special input into the net dominating the neural activity, one neuron will begin to send a sequence , it has learned earlier , using the RNA - molecules as " songbook ". ( This process mediated by Ion pumps or - channels , being regulated by the sequence of the RNA - nucleotides in the RNA - molecules ) . The neurons connected with that neuron may registrate this sequence. They may synthesize in real time an according RNA - molecule and then look by means of detection of homologuous molecules ( which is a common task in genetic and immunological processes ) for RNA molecules with a homologuous ( beginning - ) sequence ( and most probably best fitting further sequence ), they have synthesized earlier .Using these molecules , they could tune in and send activity fitting to the developping pattern into the net . By and by all neurons could be caused " to sing one song " , to reproduce one pattern ( which may win upon other competiting starting patterns ), using memory molecules in a self - organizing process . Each neuron could make its own contribution to the developping patterns , comparing the produced memory - molecules with earlier produced ones , using those to give the produced pattern its own specific modulation and completion . Thus the memory of the net would be associative . Also the reversed input of recorded temporal activity may reconstruct activity - patterns , as has been shown for wave - transducing media ( Fink 1996 ).
Of course , these considerations are speculative . But all means neurons need to perform such procedures are not far from being conceivable .

5 . Resemblances to biological neural networks :
Planar and spatial neural networks based on fractal algorithms show morpho-logic and functional correspondences ( in the reflection of fundamental aspects of development and function ) to biological neural networks :
In both we may find :
· biomorph symmetrical structures like lobes and hemispheres ,gyri and sulci and cavities similar to ventricles ; the axons of neurons projecting massive parallel , " somatotopic " , some crossing the median line in form of a decussatio ( fig. 5b).
· each neuron being connected to almost all other neurons by only few functional interneurons ( fig. 4.10 ).
· periodic and aperiodic orbits as basis of deterministic chaotic activities in biological nervous systems ( Freeman 1987) as well as in fractal functions, the visualization of functional parameters in fractal nets
resembling to pictures we get by neuroimaging procedures .

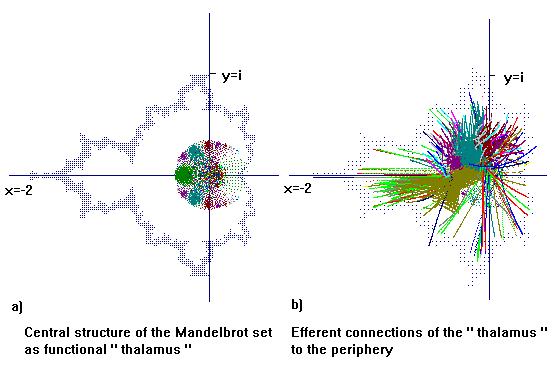
Figure 5 : Central structure of the Mandelbrot set ( values near zero , which occur in the periodic orbits) in structure and function analogue to a " Thalamus " with distinct "nuclei " ( fig. 5a) , specific efferent connections to the periphery shown for "neurons" with y*i > 0 , demonstrating the " Decussatio " of some " Fasciculi " , crossing the median line , resembling to biological thalamic connections ( fig.5b).

· activation patterns developping in the course of recurrent projections between peripheral "cortical" and central "thalamic" structures . An according central structure we can find in the Mandelbrot set in which each region has its own periodic sequences coming with a certain frequency relatively close to zero. From these " neurons " of the central structure near zero , the activity will be projected to the periphery again ( Fig. 5 ) . Like the Thalamus , this central structure of the Mandelbrot set consists of distinct " nuclei " .
· information processing being a task of the entire network .
· the possibility to activate the entire net from a circumscribed region ( near an attractor of f(1) by the recurrent projections of the reversed function in fractal nets , from some hippocampal regions in human brains in epileptic seizures )
· wave functions playing a role in network function .
· existence ( or at least possibility ) of associative memory functions .

In ontogenetic development of organisms the orientation of growing axonal fibres in fields of concentration gradients of different neurotrophic growth factors could reflect the course of trajectories in fractal functions. Thus neurons and their axons may form spatial neural networks , based on specific fractal algorithms .

6. Conclusion :
The specific fractal characteristics enable these networks to perform a new kind of data - processing. Their macroarchitecture is defined by fractal algorithms. On the microstructure they may use the principles of conventional neural networks to modulate the response of each neural column according to learning history of the network . Each signal will pass many small neural networks ( in form of the neural columns) on its way through the entire network which therefore acts as a net of nets .
The abstract structure of the networks is dialectic by manifold binary trees in which the activity is propagated in wave fronts , whose interference allows the entire network to take part in the processing of data .There are remarkable correspondences to biological neural networks , which may be due to reflecting the principles of fractal algorithms in morphogenetic events . Further investigations on these structures promise to offer a chance to produce a new kind of neural networks and to improve our knowledge about function and structure of biological nervous systems .

References :
Babloyantz A , Louren¸o C ( 1994 ) Computation with chaos : A paradigm for
cortical activity , Proc Natl Acad Sci USA , Vol 91 pp 9027 - 9031 , Biophysics
Birbaumer N , Schmidt RF (1996) Biologische Psychologie, p 598 . Springer Berlin
Destexhe A (1994) Oscillations , complex spatiotemporal behavior , and information
transport in networks of excitatory and inhibitory neurons.
Physical Review E , Vol 50 Nr 2 : 1594 - 1606
Fink M (1996)Time reversal in acoustics , Contemporary Physics 37 , 2 : 95 - 109
Freeman WJ ( 1987) Simulation of Chaotic EEG Patterns with a Dynamic Model of
the Olfactory System .Biol Cybern 56 : 139-150
Mandelbrot BB ( 1982 ) The Fractal Geometry of Nature . Freeman , San Francisco
Pieper H (1985) Die komplexen Zahlen . Deutsch , Frankfurt a. Main
Peitgen HO, Richter PH ( 1986 ) The Beauty of Fractals - Images of Complex
Dynamical Systems . Springer , Berlin Heidelberg
Wu J , Cohen L, Falk C (1994) , Science 263 , 820 - 823

e-mail:Thomas.Kromer@t-online.de