Fractals are unusual geometric structures that can be used to analyze many biologic structures not amenable to conventional analysis. The purpose of this exhibit is to teach some of the fundamentals of fractal analysis, and to show how they can be applied to analysis of trabecular bone.

Simple models of biologic structures can be constructed with simple shapes such as lines, circles, spheres, and simple polygons. One can then estimate properties of the structure, such as length, area, volume, strength, etc.

The earth could be modeled as a sphere, while an artery can be modeled as a hollow cylinder.

However, there are many complex biologic structures that cannot be easily modelled by simple shapes such as these. One of the most common such patterns is the branching structure of many biological structures. Branching structures in the human body include the arteries, veins, nerves, the Bundle of His, parotid gland ducts, and the bronchial tree.

Other Fractal Processes in Nature

• Regional distribution of pulmonary blood flow

• Pulmonary alveolar structure

• Mammographic parenchymal pattern as a risk for breast cancer

• Regional myocardial blood flow heterogeneity

• Fractal surfaces of proteins

• Distribution of arthropod body lengths

Fractal objects have several interesting properties. One of the most interesting is self-similarity. The Sierpinski triangle below is a good example of this. The big triangle is composed of four smaller triangles, each of which are composed of four even smaller triangles, ad infinitum. A fractal object such as this exhibits this self-similarity over many scales of observation, from the full-sized object down to the microscopic level.

Another property of a fractal object is the lack of a well-defined scale. A good example of this is seen in clouds, which tend to look very similar no matter what their size. Another way to state this is that it is difficult to tell just how big a cloud is without some external reference.

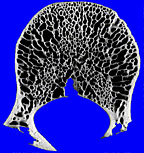
Trabecular bone has a branching pattern, as seen in this vertebral specimen. One can also see that it exhibits self-similarity. That is, the trabeculae and the marrow spaces between them look very similar no matter what their size.

It is now time to talk about the concept of a fractal dimension. Most people are familiar with the three spatial dimensions that we live in. These dimensions are known as topological dimensions, and have been used for many years to describe the shape and position of objects. Benoit Mandelbrot, however, found that certain geometrical objects couldn't be described well with the usual topological dimensions, and formulated the idea of a fractional or fractal dimension, existing somewhere between the usual topological dimensions.

Each of the following objects has a topological dimension of 1. However, the more complex they become, the more they tend to fill the space about them. The amount of space filled by one of these objects is represented by the fractal dimension or index (D), which can be thought of as a "filling factor".

For the line and circle, D is equal to 1.0. The snowflake pattern on the right fills more space than the line or circle, and its D is 1.26.

The Koch fractal above fills even more space than the snowflake pattern, and has a D of 1.5.

The fractal dimension ranges between 1 and 2. It is 1 where the structure is a simple straight or curved line, and fills almost no space. When a structure fills all available space, such as the yellow square below, its fractal dimension is 2.

Many past models of bone have confined themselves mostly with modelling breaking strength as a simple function of bone mineral density. Bone density is certainly strongly related to breaking strength. However, there are wide biological variations seen in breaking strength among patients with the same bone density. Therefore, investigators have sought to create more refined models of bone strength.

Some of these models are based on the idea that it's not just how much mineral you have in a given bone, but also how it's arranged within that bone that determines bone strength. Indeed, finite element analysis models of bone strength have been fairly successful in predicting bone strength. However, these models are quite complex, and are unlikely to become clinically useful for a given patient in the near future. The idea that the fractal index of trabecular bone might be related to bone strength is an appealing one, since the fractal index is simple to calculate from clinical CT images of a given bone.

The image below shows two possible models for bone. Normal bone lies somewhere between the hollow cylinder of bone on the left and the solid cylinder on the right. If one analyzes CT slices of these two bones, one would measure a fractal index of 1.0 on the hollow bone and an index of 2.0 for the solid bone. Measurements of normal bone fall somewhere between these two extremes (about 1.7 - 1.8), and it is plausible to hope that the fractal index may prove useful in estimating bone strength.

Bone with no trabeculae ("osteoporosis") D = 1.0		Bone with solid center ("osteopetrosis") D = 2.0

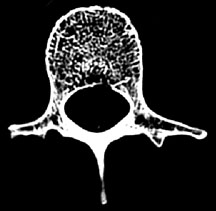
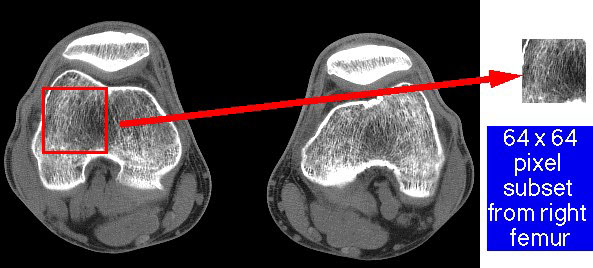
How then, does one estimate the fractal index of a complex fractal structure like the trabecular bone in the vertebra above?

We first need to tell our image analysis program which tissue is bone and which is not. This is generally simple since bone is far denser than soft tissue. In our image analysis program, we adjusted the window and level controls so that only tissue with CT density greater than a certain level would be included in the analysis. This can be done visually in our software by adjusting the window and level controls until only the tissue of interest is shown in red, as below.

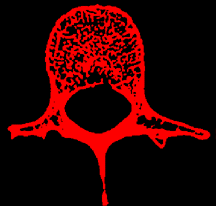
Once these threshold levels have been set, the imaging software now knows what is bone and what is not. One can now use the region of interest cursor to select an appropriate section of trabecular bone to analyze, as shown below.

Algorithms for Estimating the Fractal Index

There are a wide variety of computer algorithms for estimating the fractal index of a structure, such as the box-counting algorithm, the pixel dilation method, the calipher method, the radial power spectrum method, and others. We will demonstrate the box-counting algorithm, because of its simplicity.

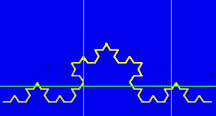
This algorithm estimates how much of the available space is taken up by the fractal structure. First, an arbitrary grid is placed over the structure to be measured. Then, one counts how many boxes in the grid are filled by the fractal structure. For the grid size above, the structure fills 6 boxes.

The process is then repeated with a grid half the size of the previous one. With the grid below, the structure fills 9 boxes.

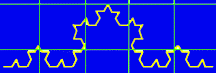
The process is again repeated with a grid half the size of the previous one. With the grid below, the structure fills 18 boxes.

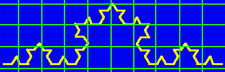
This process can be carried on indefinitely, using smaller and smaller grids. For this demonstration, we will only count the boxes one more time. With the final grid below, the structure fills 59 boxes.

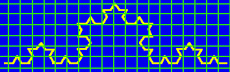
So, our box-counting data is summarized in the table below:

The data from these four countings are tabulated and plotted on a log-log plot as shown below. A linear regression is done to find the best fit. The slope of this line is used to calculate the fractal index. The best fit equation is y = -.84x + 7.8

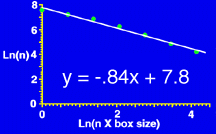
This fractal index is equal to 1 minus the slope of this line. Thus, for this fractal object, the fractal index D = 1 - (-.84) = 1.84

This concludes our exhibit on fractal analysis. We hope that you have found it of interest.