For the past few years, I have been applying the analytic thinking of a scientist to find basic laws for architecture and urbanism, following the lead of my friend, the brilliant architectural theorist Christopher Alexander. The results derived so far show that a building, or city, is subject to the same organizational laws as a biological organism and a complex computer program (1). The New Architecture depends upon scientific rules rather than stylistic dictates. Using these rules, we can create new buildings that duplicate the intensely positive, nourishing feelings of the greatest historical buildings, without copying neither their form nor their style.
Great buildings of the past, and the vernacular (folk) architectures from all around the world, have essential mathematical similarities. One of them is a fractal structure: there is some observable structure at every level of magnification, and the different levels of scale are very tightly linked by the design. In contradistinction, modernist buildings have no fractal qualities; i.e., not only are there very few scales, but different scales are not linked in any way. Indeed, one can see an unwritten design rule in the avoidance of organized fractal scales.
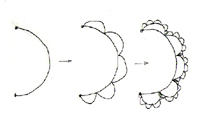
Generating a mathematical fractal on different scales.
We also see this type
of structure in traditional buildings. All the folk architecture built by
people around the world tends to have fractal properties. I believe that
our mind is "hard-wired" to construct things in a certain way, so
inevitably we build fractal structures. Most great creations of humankind
go far beyond strictly necessary structure; we feel a need to generate
certain types of forms and geometrical interrelationships. Only when
influenced by some style do we depart from what comes naturally to
us.
Cities --
at least the most pleasant ones -- are fractal. Everything, from the paths
and streets, to the shape of fašades and the placing of trees, is fractal
in the great cities such as Paris, Venice, and London. This has been
measured mathematically by people like Michael Batty and Pierre
Frankhauser.
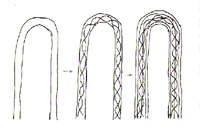
Fractals have two
related characteristics: they show complexity at every magnification; and
their edges and interfaces are not smooth, but are either perforated or
crinkled. A fractal has some connective structure at different scales.
Historical cities are richly structured at every magnification, whereas
contemporary cities enhance the largest scale but suppress everything
else.
There
are no straight lines in fractals. A smooth flat plane has no
substructure, and is therefore non-fractal. Colonnades, arcades, rows of
narrow buildings with cross-paths all correspond to a permeable membrane
with holes to allow interchange -- this is one type of
fractal.
When
an urban interface is not permeable, it is convoluted, like a crinkly
meandering river or folded curtain. A building edge couples by
interweaving with its adjoining space, creating another type of fractal.
This folding arises spontaneously as a natural consequence of urban
forces; for example, portions of buildings that grow outwards onto the
pavement. Despite the obvious threat to public space, it seems that this
process represents a natural evolution of the built boundary into a more
stable fractal form.
I'm sure that that occurs because what we understand as order in a
city has to do with the largest scale, whereas human beings connect to the
human scales. The most important urban structures exist on much smaller
scales, going right down to the detail in the materials.
One of the stated aims of
modernism was to eliminate any architectural interface with fractal
dimension. These were replaced by long, straight roads, and reinforced
with the strict alignment of buildings. The reason given was to clean up
the perceived messiness of older cities; yet that messiness was really the
organized complexity that made them alive.
Imagine the range of fractal
interfaces as generated by the following mechanical model. Take a wire and
compress it longitudinally, fairly evenly along its entire length. It will
buckle and crinkle, creating a fractal boundary of dimension greater than
one. (The dimension is more than one because the line fills up some area
with its undulations, and would have dimension two if it filled in all the
area).
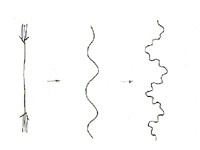
Fractal created by longitudinal compression.
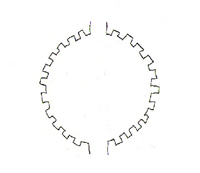
If you then pull it to straighten it out, again evenly along its length, it will first straighten, and then it will break into aligned pieces so as to be able to extend its length. This creates a fractal line with fractal dimension less than one (i.e., a line with holes in it that is closer to a collection of points having dimension zero than a continuous line of dimension exactly one).

Fractal generated by tension and breaking.
Of all possible lines
one can create in this way, the perfectly smooth, straight line has a very
low probability of occurring; and yet, that is what architects try to
enforce all over the world. Traditional villages show an infinite range of
fractal interfaces between their building fronts and street. There, one
finds gentle curves that are crinkled on the small scale, and lines that
are only approximately straight on the large scale.
Even in formal planning, a
curved structure such as the Circus and Royal Crescent at Bath arises from
compression, and so it is crinkled on the human scale. The opposite is the
colonnade and arcade, which comes from tension, and is straight. Even
though there exist curved colonnades, such as St. Peter's, I believe that
they are far less successful than structures that follow this
model.
Curvature arises from longitudinal compression.
Another point is the scale on which the fractal dimension is measured: great urban environments use fractals on the human scale, whereas dead environments deliberately remove them. For example, a colonnade is useful when the intercolumn spaces are roughly between 1m and 3m, i.e., comparable to the human scale of movement.
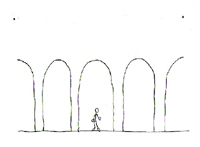
A portico is a fractal on the human scale.
Monstrous spaces of more than 5m between columns alienate the user. For this reason, flat, smooth buildings that are aligned and spaced 20m apart may resemble a fractal line on paper, but they so far exceed the human scale as to be totally alienating. They are not fractal on the human scale, which is what is important.
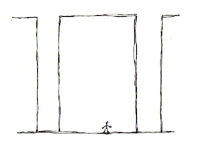
Non-fractal structure suppresses the human scale.
While the New
Architecture does not address ecology per se, it does lay the
groundwork for an ecological approach to planning and building. We have
been discussing how scientific laws establish the connectivity of man to
his environment, which occurs through fractal qualities of structures.
Natural structures are fractal, whereas only traditional buildings are
fractal. Modernism teaches us to eliminate fractal structures and to
replace them with non-fractal built structures. This philosophy does not
respect a tree or an older building. As soon as we realize that we connect
only to fractal structures, we will reverse our priorities, and appreciate
a tree more than a modernist glass cube. Only then will we think twice
about replacing the former with the latter.
Architecture and Urban Design
are at an impasse, because the rules that students are taught in schools
contradict the structural organization of living forms. The fractality of
older cities has been deliberately erased in order to impose certain
arbitrary stylistic rules. This has led to the philosophical,
psychological, and physical separation of human beings from their
environment. Protests from ordinary people that architects and urban
planners are deliberately destroying comfortable and emotionally
nourishing human environments have had little effect. We are building our
cities into places that are hostile to human activities. Look at a
contemporary city -- it fails miserably as an environment for children
from infants to teenagers. Environmentalists increasingly blame architects
for damaging the natural environment, but the damage extends far
deeper.
Information provided
by:
http://sphere.math.utsa.edu/sphere/salingar/urbanstructure.html