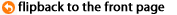|
UA Mathematicians Predict Patterns in Fingerprints,
Cacti
By Kara Rogers
March 31, 2004
Patterns in nature can be seen every day, yet in many
cases, little is understood about how and why they form. Now University of
Arizona mathematicians have found a way to predict natural patterns,
including fingerprints and the spirals seen in cacti.
UA graduate
student Michael Kuecken developed a mathematical model that can reproduce
fingerprint patterns, while UA graduate student Patrick Shipman created a
mathematical model to explain the arrangement of repeated units in various
plants. Shipman's report on his work will be published in an upcoming
issue of Physical Review Letters.
Even though the use of
fingerprints for identification began more than 2000 years ago in China
and they have been studied experimentally for over two hundred years,
there is no widely accepted explanation for their occurrence. Likewise,
the reasons behind nature’s choice of patterns in plants have been
difficult for mathematicians to explain, despite these patterns having
been identified centuries ago.
“What I like about this research is
the interplay between math and biology. It is actually quite difficult,
because the disciplines require a somewhat different mindset and biology
is notoriously bewildering and full of detail,” Kuecken said. “In a way,
dealing with this problem was like putting together a jigsaw puzzle of
facts. I had to try out different things and could use math, and sometimes
common sense, to see if the pieces actually fit.”
Human skin has
multiple layers, including the outermost epidermis and the inner dermis.
The outer and inner layers are separated by the basal layer, which is
composed of cells that constantly divide. Growth occurs in a similar
fashion in plants, which have areas of continuous cell growth, such as the
tip of a cactus, that allow the plant to grow larger.

Human fingerprint
patterns are created because basal skin grows faster than surface
skin, which then buckles, forming ridges. |
The basal layer in human skin and the equivalent layer
in plant skin grow at a faster rate than either the surface layers or the
thick dermis layer. As the basal layer continues to grow, pressure
increases. In both plants and fingertips, the growing layer buckles inward
toward the softer inner layer of tissue, relieving the stress. As a
result, ridges are formed on the surface.
The undulations from the
buckling form fingerprints and various patterns in plants, from the ridges
in saguaro cacti to the hexagons in pineapples. The way a pattern is
formed, regardless whether it is a fingerprint or a plant, is related to
the forces imposed during ridge formation.
The basic properties
responsible for the mechanism of buckling in plants and fingerprints
happen in other materials as well. Kuecken and Shipman's graduate advisor,
UA professor of mathematics Alan Newell, said, “In material science,
high-temperature superconductors seem to be connected with stresses that
compress to build the structures in various high-temperature materials.
Indeed, the idea that buckling and surface stresses would have something
to do with the patterns you see in plants is fairly recent.”

Kuecken developed
a mathematical model that can generate patterns like this one, which
looks like a fingerprint. |
In fingerprints, ridge formation is influenced by
discrete elevations of the skin on the fingertips, called volar pads,
which first appear in human embryos at about six and a half weeks. The
volar pads' location is where the epidermal ridges for fingerprints will
arise later in development.
Kuecken explained that as the volar
pads shrink, it places stress on the skin layers. The ridges then form
perpendicular to this stress. There are three basic patterns of
fingerprints known as arches, loops and whorls that form in response to
the different directions of stress caused by shrinking of the volar pads.
Other research on ridge formation has already shown that if a person has a
high, rounded volar pad, they will end up with a whorl pattern. Kuecken's
mathematical model was able to reproduce these large patterns, as well as
the little intricacies that make an individual fingerprint unique.
Shipman’s model, like Kuecken’s, also took into account stresses
that influenced ridge formation. In plants, forces acting in multiple
directions result in complex patterns. For example, when buckling occurs
in three different directions, all three ridges will appear together and
form a hexagonal pattern.
“I’ve looked at cacti all my life, I
really like them, and I’d really like to understand them,” Shipman said.
To study these patterns, Shipman looked at the stickers on a cactus or
florets on a flower.
When a line is drawn from sticker to sticker
on a cactus in a clockwise or in a counterclockwise direction, the line
ends up spiraling around the plant. This occurs in many plants, including
pineapples and cauliflower. When these spirals are counted, it results in
numbers that belong to the Fibonacci sequence, a series of numbers that
appears frequently when scientists and mathematicians analyze natural
patterns.
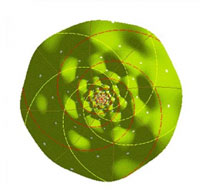
Shipman found
that cactus stickers predicatably align in spiral
patterns. |
From his model, Shipman found that the initial curvature
of a plant near its growth tip influences whether it will form ridges or
hexagons. He found that plants with a flat top, or less curved top, such
as saguaro cacti, will always form ridges and tend not to have Fibonacci
sequences. Plants that have a high degree of curvature will produce
hexagonal configurations, such as those in pinecones, and the number of
spirals will always be numbers in the Fibonacci sequence.
Newell
says that Shipman's mathematical model demonstrates that the shapes chosen
by nature are those that take the least energy to make. “Of all possible
shapes you can have, what nature picked minimizes the energy in the
plant.”
|