Abstract

In human consciousness a world of separated objects is perceived by an inner observer who is experienced as an undivided feeling of one-self. A topological correlation of the self to the world, however, entails a paradoxical situation by either merging all separated objects into one or splitting the self in as many disconnected sub-selves as there are objects perceived. This study introduces a model suggesting that the self is generated in a neural network by algorithmic compression of spatial and temporal information into a fractal structure. A correlation of an inner observer to parts of a fractal structure inevitably entails a correlation to the whole, thereby preserving the undividedness of the self. Molecular mechanisms for the generation of a fractal structure in a neural network and the possibility of experimental investigation will be discussed.

Introduction

Consciousness has remained to be an enigmatic property of the human mind since its nature was discussed in the early days of philosophy. The most elusive phenomenon observed with consciousness is its ability to generate an inner imagination or view of the outer world. It is based on a very common sense experience of a "thinking thing" inside our mind though unprovable by critical scientific analysis. A lack of appropriate scientific means to analyze human consciousness results in the view that mind function is reducible to mere electro-physiological mechanics of the nervous system. Reductionistic models are useful in explaining the computation of nerve signals by specialized areas of the brain but are not able to explain the integration of conscious experience emerging from these signals. The simultaneous perception of spatially or temporally distinct information apparently does not destroy the feeling of an undivided self as being the only observer aware of the inner world (Baars J., 1997; Strawson G., 1997). The experience of the self in a one-to-all correspondence can be established by the principle of fractality. In a fractal structure iterative pointing at one element correlates the pointing entity to the entire fractal as being a downscaled part in each of its elements. The underlying geometry has been intensively analyzed by Benoit Mandelbrot and shown to provide a general principle of structurization in nature (Mandelbrot B., 1982). The present study discusses a model for application of fractality to integration of information perceived in consciousness in order to explain the preservation of an undivided inner observer, the self. An underlying algorithm for fractal integration will be developed and correlated with a neurophysiological process in the nerve cell membrane. On basis of this process an experimental approach for the investigation of a putatively fractal structure in the nerve cell membrane will be suggested. The following sections will be composed of discussion parts and more detailed mathematical descriptions. For brief reading, the mathematical analysis can be skipped without loss of crucial information.

Results and Discussion

The self and the world as a topological space

In order to install an algorithm for the description of the self and the topology of consciously perceived spatio-temporal information we have to develop a symbolic notation which is able to cope with a standard mathematical form. (The operations and and or will be used for "union" and "intersection" as in set theory or according to the equivalent symbols in Boolean logic, respectively).

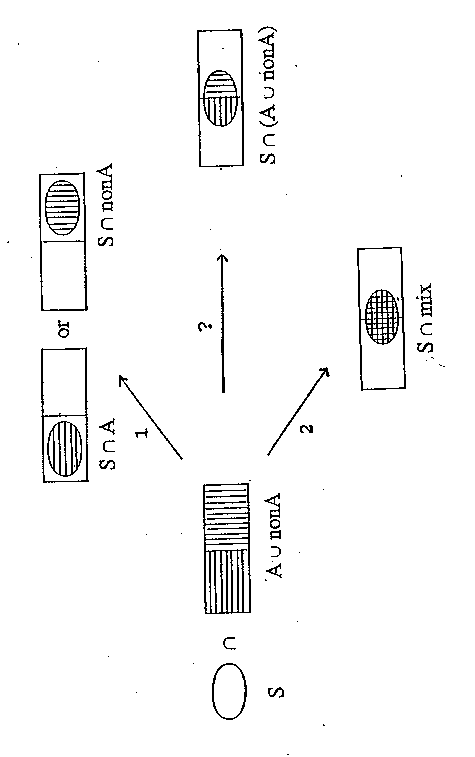
Suppose that the self can be defined as a set S with only one member: S itself. S is introduced as a quality in order to have a variable which can be included into an algorithmic description. The first premise for the definition of S is that it has to be an irreducible entity which under any operation cannot be divided into different sub-selves. Nevertheless, S is the entity in each of us which is able to perceive all objects, sensations and emotions we are aware of in our consciousness. Now suppose there is a topological space X in which this information is distributed. We will define a group of spatially distributed sensations as subset A being disjointed from the complement subset nonA. Accordingly, the intersection of A and nonA will form an empty set: A and nonA = 0. As shown in Fig. 1, a one-to-one correspondence of S to A or nonA leads to two putative solutions each of which being contradictory to the initial properties of S or A or nonA, respectively. Solution 1 favors either the combination S and A or S and nonA. Since A and nonA are complementary and in turn disjointed subsets in X, the topological space will become disconnected referring to the embedded subset. Depending on which information S is focused on it will also be embedded in the respective and in turn distinct subspace or it will be split into two disjointed subsets s₁ or s₂. This implies the logically contradictory situation: S unequals S. On the other hand, solution 2 will preserve the undividedness of S but in consequence abandons the spatial difference between A and nonA. This also implies a contradictory situation in which a homogeneous mixture of sensations is experienced: A equals nonA. The logical dilemma arises from the attempt to apply the distributive law to the expression S and (A or nonA) which will inevitably reduce S to the correlation S and A or S and nonA. A solution of this dilemma is possible if a part of a geometrical object is always composed of a downscaled version of the entire structure. Pointing at one element entails inevitably correlation to the whole. Applied to S, a correlation to A or nonA preserves its undividedness since any attempt to reduce S by correlation to a part iteratively re-establishes a one-to-all correspondence. The scale-invariance of correlation is known to be realized by generation of a fractal structure and will be evaluated in the following mathematical section.

________________________________________________________________

Mathematical analysis 1: Scale-invariance of correlation in fractal structures:

Solutions 1 and 2 in Fig. 1 will be expressed in terms of operator functions on S in order to resolve the logical contradiction to the initial conditions by generation of the self. The logical states A and nonA will be merely characterized by the ability to cover sub-spaces x_i of X. By definition it follows that x₁(A) or x₂(nonA) = X, and x₁(A) and x₂(nonA) = 0. The simultaneous realization of the two logical states will be described by a linear superposition with f, g and h acting as operator functions on S:

f{S and X} = g{S and A} + h{S and nonA}; Eq. 1

The undividedness of S will now be preserved by the introduction of a scaling operator z such that S remains invariant under scaling by z:

f{S and X} = f[z {S and x₁(A)}] = f[z {S and [x₁(A) or x₂(nonA)]}]; Eq. 2

The realization of the scaling invariance of S will be approached by a construction of X according to self-similar or fractal structures. A general algorithm for the description of fractals develops from the idea that in self-similar structures there is always the same correlation between the size of pieces x and their number N(x) (Peitgen H.-O. et al., 1992). This correlation can be interpreted in the sense that the entire structure perceived by the self is a scale-invariant magnification of each part of it. A possible solution for equation 2 with x = S and X is then given by a the following power law (Liebovitch L.S. and Toth I., 1990):

f(x) = C x^(1-D); Eq. 3

where, C is a constant and D = lim(x to 0) [logN(x)/log(1/x)]

The fractal dimension D is a constant for the geometrical description of self-similar structures (Peitgen H.-O. et al., 1992).

In the present context the power law describes the topological scale-invariance of the dyadic combination S and X.

________________________________________________________________

In Fig. 2A the principle of self-similarity is illustrated by iterative tiling of a plane giving rise to the construction of a Sierpinski triangle. A particular feature of fractal tiling is again given by the principle of scale -invariance: a correlation to one tile by iterative downscaling entails a scale-invariant correlation to the entire structure. It is just this property of the fractal concept which provides a solution for the correlation of S to distinct tiles under preservation of its irreducibility. There is, however, one crucial pitfall in any iterative downscaling operation. No matter how small the tiles are, they are still separated. Infinite downscaling operations require an infinite structurization of space and time which is hard to imagine for a physical substrate. Instead it is assumed that there is a spatial state reached by finite downscaling when the fractal is composed of separated but yet "connected" (not independent) states. The connectedness can be realized by engaging spatially separated states in an intermediate pre-state of not being A or nonA, but temporally synchronizing a subsequent manifestation of the two states. This phenomenon of fractal coherence will be described by a combination of eqs. 1 and 3, with x = S and X and X = x₁(A) or x₂(nonA), which establishes a scale-invariant and non-distributive correlation of S to X:

f{S and X} = C {S and [x₁(A) or x₂(nonA)]}^(1-D) ; Eq. 4

It should be emphasized at this point, that the term fractal coherence is introduced as a mere mathematical construct in order to meet the principles of scale-invariance and non-distributiveness. We will now evaluate how this operation for fractal construction might be realized in our brain (or in any appropriate physical environment).

The tiling of the world in our mind

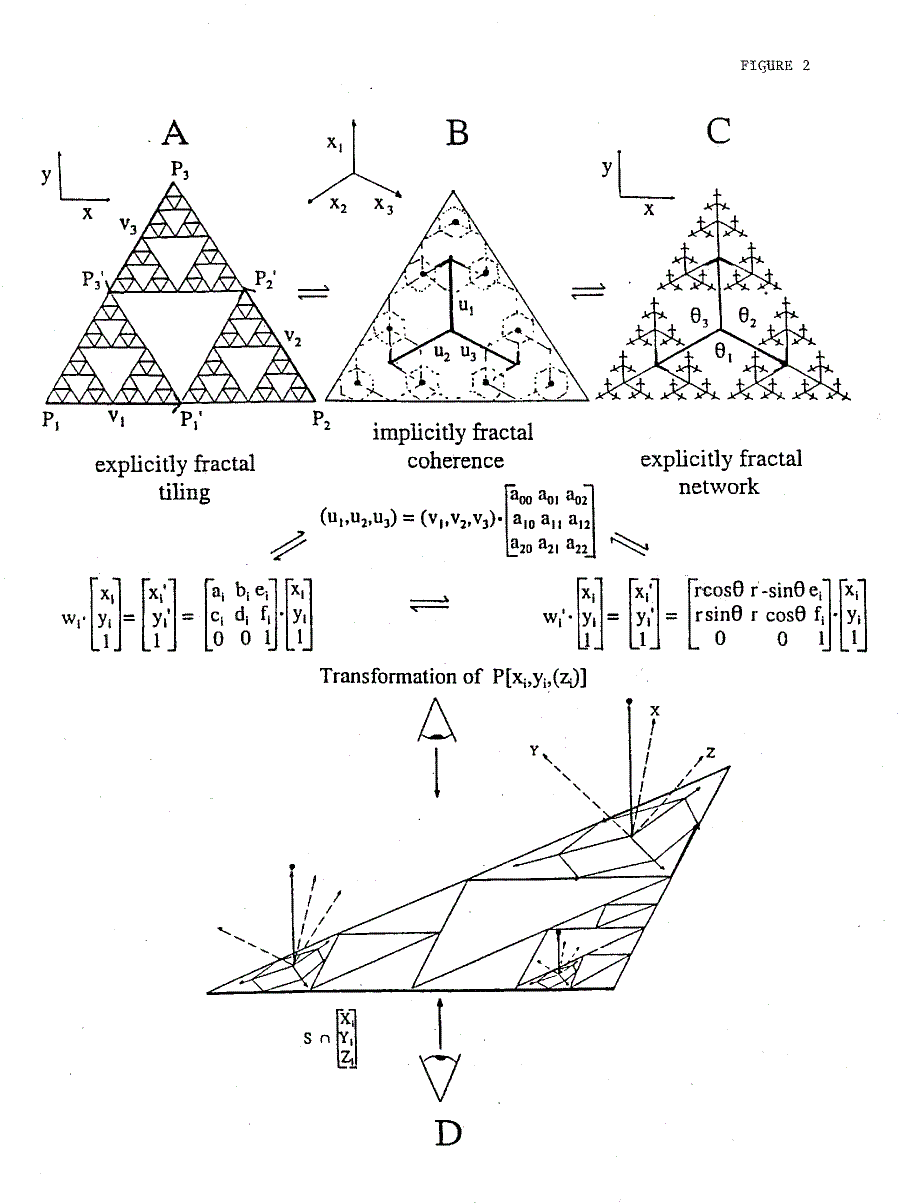
In order to describe the construction of a fractal structure in a neurophysiological substrate it is necessary to define an construction algorithm compatible with the physical properties of this substrate. It should be noted, however, that the primary goal of this section is to develop a figurative but still completely abstract algorithm for the realization of spatial information perceived in our consciousness. A putative correlation to a neurophysiological substrate will be discussed in the following sections. A general directive for the construction of fractal structures is given by a specific affine linear transformation w_i(P_i) of n points P_i in a metric system R(N), with N = spatial dimension (Peitgen H.-O. et al., 1992). A transformation w generating self-similar structures by iterative downscaling is given by the Hutchinson operator (Peitgen H.-O. et al., 1992). The application of this operator on different geometrical directives for spatial distribution of points is able to entail the generation of fractal structures which are transformable into each other. Figure 2 illustrates this equivalence for the Sierpinski triangle which can be constructed by iterative rotation and contraction of a triangle in a plane (Fig. 2A), or by a tree like network as in Fig. 2C. The fractal is implicitly contained within a modified version of the "Apollonian gasket" generated by a distribution of hexagons shown in Fig. 2B (see Fig. 3 for comparison). The equations underneath the figures are of descriptive nature derived from the algorithmic similarity for the construction of different fractal structures (Peitgen H.-O. et al., 1992). A comparison of the Sierpinski triangle (Fig. 2A) with the modified (hexagonal) Apollonian gasket (Fig. 2B) indicates a construction directive for the spatial adjustment of signal flow by linear affine transformations in order to generate a fractal in a neural network.

________________________________________________________________

Mathematical analysis 2: Spatial adjustment of signal flow for fractal construction

A covariant component of the input vector v_i' is iteratively subtracted until the output vector v_i is orthogonal to u_i. This computational process is similar to a model introduced by Pellionisz and Llinas for signal adjustment of sensory input to executive motor output vectors in the cerebellum (Pellionisz A. and Llinas R., 1980). By this adjustment the system of u-vectors is consistent with the construction of the Sierpinski triangle by a tree like network with the enclosed angles determining the direction cosines (Fig. 2C). It should be noted for purpose of generalization that the network construction of the fractal is again directed by a linear affine transformation, this time derived from a more convenient polar coordinate notation. Linear affine transformation is driven by rotation (by angle as indicated in Fig. 2) and translation of a triangular plane in each step of iteration.

________________________________________________________________

The equivalence of the Sierpinski triangle to a tree like network establishes the spatial adjustment of the affine transformation as a process "growing" by time. This property is most remarkable as it is in accordance to the distribution of information in neural networks with dendritic structure (Peitgen H.-O. et al., 1992). Once the network splits into sufficiently small branches coherence occurs as described in the preceding section. In Fig. 2B, it is illustrated the simultaneous effect of three signal vectors u_1-3 on one point element surrounded by a hexagonal area under coherence. This array will be defined as the smallest fractal d{SX} representing the elementary tile for the construction of space perceived in consciousness. The metric underlying the elementary tile d{SX} can be formed by a coordinate system with the principle axes x_i lying in the plane enclosed by the tile (see Fig. 2B). In the case of the Sierpinski triangle the vectors u_i pointing to the vertices are collinear to x_i. Rotation will superimpose them irrespective of the construction directive applied (Fig. 2A or C). In order to describe the perception of space by an inner observer it is suggested that these vectors generate the three components X_i,Y_i, Z_i for one point in a three-dimensional space perceived by the self. As illustrated in Fig. 2D the respective operation "lifts up" the spatial information given by the fractal in R2 to a point seen in R3. The eye in Fig. 2D representing the self as the inner observer of visual information adopts a dual position in either R2 or R3, thereby indicating a general consideration for any RN. As shown in Fig. 2D the components of any point perceived in consciousness are subject to transformation to a coordinate system opposite to the position of the observer. Adjacent tiles don't simply fuse in a coherent area of homogeneously mixed information (equivalent to Solution 2 in Fig. 1) but superimpose their texture without giving up their individual spatial distribution. Each elementary tile behaves like a "point", but forms a connected space with other tiles covering the entire coherent lattice. The size of adjacent fractals may vary depending on the actual coherence length. This does not violate the principle of self-similarity, but gives rise to points in R3 with different distance to R2 and may distribute them in a three-dimensional space as it is experienced in our mind. It should be emphasized that the space perceived in consciousness is not to be assigned to an Euclidean space somewhere in brain. In fact, the directive suggested for construction of this "hyper"space (see Fig. 2D) implies the impossibility to form a common space with the vectors used for its generation in a neurophysiological substrate. Instead, it is only possible to investigate the neuro-physical principles underlying this construction in an experimentally accessible Euclidean space. The hexagonal version of the Apollonian gasket is meant as an approximation for a model structure generated in a neuronal substrate coping with fractality as well as coherence. We will now evaluate how the transformation from a fractal network to a neuronal substrate under coherence may develop.

Principles of fractal coherence

The distribution of the self to the elements of a fractal structure is attempted by a probabilistic approach derived from the theoretical basis of the generation of fractal images (Peitgen H.-O. et al., 1992). According to this model the spatial distribution of the self (equivalent to the image density) is depending on the distribution density of the preceding image (pre-image). This approach appears to be justified since fractal distribution follows a certain path determined by the self-similarity in each step of construction. The construction directive applied is called Markov process and can be expressed for any type of fractal structure. The advantage of this process is given by a spatial adjustment of signal flow (by Hutchinson operation) reacting to the actual signal distribution in each step of iteration. Iterative distribution of signals or the self onto downscaled space intervals will proceed until the spatial limit for coherence is reached. The distribution density of S derived from the Markov operation will then be transformed to that of the space under coherence. A mathematical analysis will show that a Markov operation can be converted to a quantum computational process relying on the equilibrium density of the coherent state.

________________________________________________________________

Mathematical analysis 3: Conversion of a fractal to a coherent state

Suppose that in a pre-coherent state t<t_c the self S hits the space intervals dx₁=x_c-x₁ and dx₂=x₂-x_c with the probabilities p₁(dx₁) and p₂(dx₂). The distribution of the self is then given by a Markov operation according to fractal image construction as described in (Peitgen H.-O. et al., 1992):

M(v) = p₁ v(S) w_-1(dx₁) + p₂ v(S) w_-1(dx₂); Eq. 4

with w(dx) = Hutchinson operator with w_-1 = pre-image on dx

v(S) = integral of {u(dx,t) dx}

u(dx,t) = distribution density of "S" on the pre-image

An iteration of w(dx) leads to a fractal distribution of S on sequentially contracting intervals of dx. After sufficient downscaling iterations, S is driven to the attractor x_c+/-dx_l which is equivalent to the point of coherence. The probabilities for the distribution of S onto dx derived from the Markov process are transformed into those for the description of a coherence equilibrium.

p(eq) = ½ (p₁ + p₂); Eq. 6

This equation resembles an algorithmic description recently introduced for quantum computation of bulk spin states (Gershenfeld N.A. and Chuang I.L., 1997). In anlogy to the non-distributive superposition of the logical states A and nonA, the coherence equilibrium of i eigenstates on each scale can be calculated in terms of energy levels a_i.

p_i ~ a_i = hf_i/(2kT); Eq. 7

(in terms of Boltzmann factor k), f_i = frequency of the wave-function).

________________________________________________________________

The mathematical analysis eventually resulting in eq. 7 indicates that the recently developed principles in quantum computation may be useful for a description of the logical superposition S and (A or nonA) in the space experienced in human consciousness. An adequate description has to take into account all combinations of space intervals with the self (e.g., with "spin up" equivalent to "hit by the self" and "spin down" equivalent to "not hit by the "self"). With N space intervals we will find a coherence equilibrium of 2^N combinations (Gershenfeld N.A. and Chuang I.L., 1997). The discrete probability for each combination will then be derived from those of the Markov process. Quantum computation as expressed by eq. 7, however, provides no proof that the energy levels are spatially distributed according to a fractal structure, that is to say: the coherence equilibrium is scale invariant. A simple power law according to a_i = const. h f_i^(1-D)/(2kT) (see eq. 3) appears not to be sufficient to justify this conclusion. The scale invariance, however, is as discussed earlier the prerequisite in the present model that a logical superposition of eigenstates results in a fractal distribution of energy nodes. In other words, for implication of a conscious experience, it is to be shown that quantum computation is based on a fractal structure implicitly contained within a space under coherence.

A neurophysiological substrate of the self

On search of a physiological mechanism in our brain which is able to generate consciousness it is crucial to find a substrate being able to build up a coherent state with underlying fractal geometry. As depicted in Fig. 2C any dendritic network may then be programmed on directing the flow of spatial information according to a fractal set-up. The undividedness of the self has often led to the impression that there is a substance under coherence in our brain. The physical description for the excitation of coherence in biological substrates was introduced by Fröhlich about thirty years ago (Fröhlich H., 1968). Recent applications of his theory to an explanation of consciousness by Hameroff, Pribram and Penrose favor the idea that it is generated by a network of neuronal microtubules forming an extended coherent phase (Jibu M. et al., 1994; Penrose R., 1994). In the present study the generation of physically extended coherent states is avoided. The connection of the self to a world perceived by it is suggested to be achieved by algorithmic compression of spatial information according to a fractal structure in a neural substrate. It should be noted, that the informational flow for fractal construction is subject to "pre-conscious" neuronal computation and can be evenly distributed to any space of the brain. This circumvents the necessity that the realization of the self is restricted to a microscopic spot somewhere in the brain. However, in order to avoid a speculation on non-local (remote) connectedness of events perceived in the human mind, the neuronal computation has to be based on each distinct information represented in consciousness. A microscopic coherent state is most likely generated under the influence of neuronal signal transduction. The nerve cell membrane is permanently subject to electro-physiological excitation owing to ion fluctuations which are triggered by transduced signals from different spatial directions. The ion fluctuations are depending on the conformational changes of ion channel proteins integrated within the nerve cell membrane and modulated by surrounding membrane lipids. Recently, a Monte-Carlo simulation of conformational coherence of membrane lipid arrays in a clustered lattice surrounding integral membrane proteins (e.g., ion channel proteins) has shown a sharp increase in coherence length at the transition temperature of the membrane (Sperotto M.M. and Mouritsen O.G., 1991). Interestingly, the phase transition temperature is extremely close to the body temperature which is often correlated with the composition of the lipids in the nerve cell membrane (Perillo M.A. et al., 1994; Becker K. and Rahmann H., 1995). For a hexagonally shaped lattice a coherence length of more than 60 was found which is consistent with a cluster area of about 10^-17 m² and hence corresponds to approximately 1/10⁸ of the total membrane surface of the nerve cell body. This model is in good agreement to the construction directive for a hexagonal Apollonian gasket as shown in Fig. 2B. A number of 10⁸ ion channel proteins (corresponding to 0.2 fmol) plus surrounding membrane arrays could build up a lattice of coherent areas on the entire membrane surface of one cell body. It is more likely, however, that a connected lattice is composed of smaller patches of lipid arrays under coherence. This assumption is consistent with recent observations on integral membrane proteins forming clustered patches (Koh et al., 1994) on the cell surface.

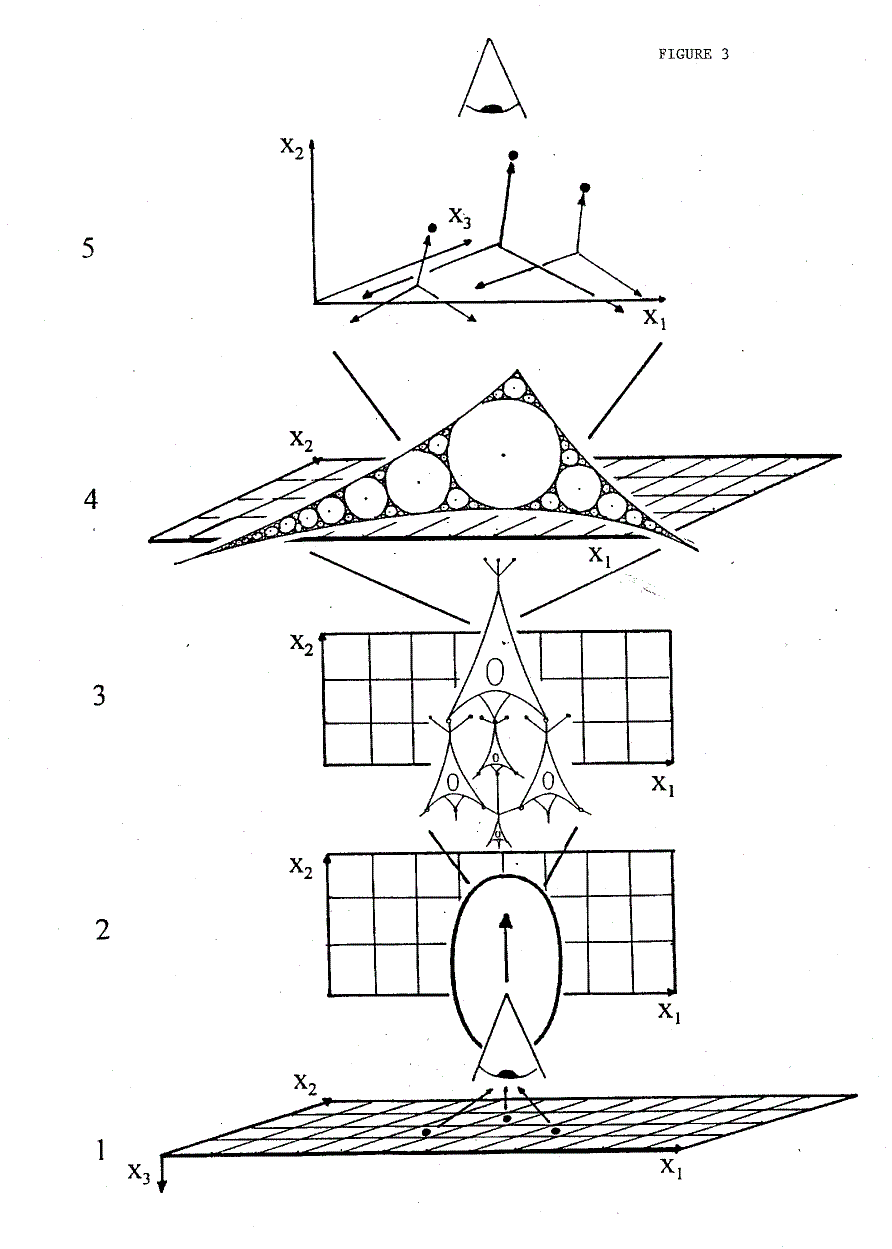
Fig. 3 summarizes the vertical signal flow through five distinct but interdependent levels of "coordinate systems" in the brain. Level 1 describes the local information of the outer world projected onto the retina and is followed by its transfer to visual centers in the brain on level 2. Each center houses a network of converging and diverging nerve connections (level 3) with the goal to integrate and compress the information onto the next level. Level 1 to 3 is fully compatible with the current reductionistic view of neuronal computation and can be intensively described by this type of analysis. Level 4 is most remarkable as it comprises the set-up mechanisms for conscious experience which still elude reductionistic description. According to the model presented here the outer world is reconstructed from the inner point of view of the self on level 5. This level represents the "hyper"space which cannot be assigned to an euclidean space in the brain, but which is constructed by neuro-physiological processes within the brain. We will now discuss how this process can be evaluated by experimental investigation.

Experimental investigation of fractal coherence in neuronal networks

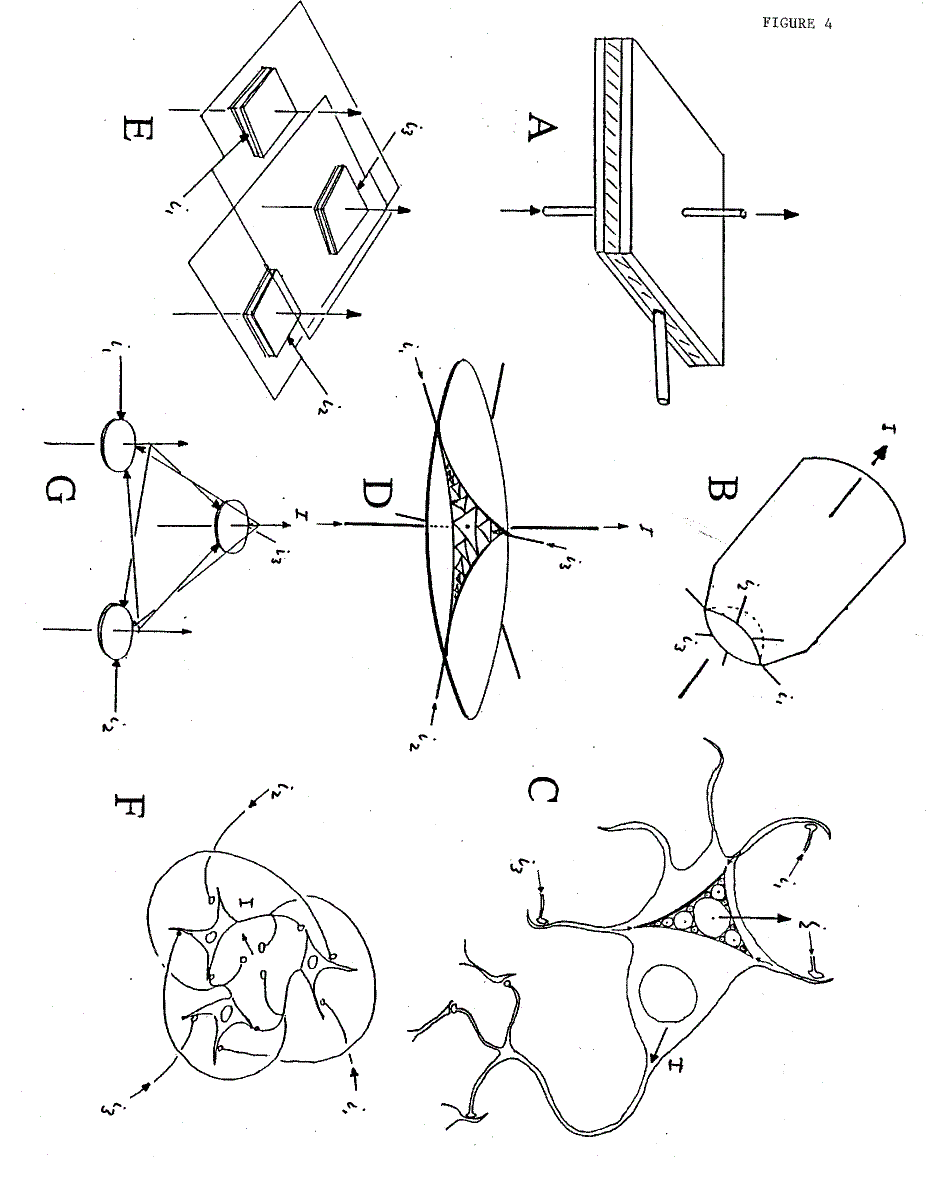
The creation of fractal coherence in a neuronal network is suggested to provide an experimental approach to investigate neurophysiological processes underlying consciousness in human mind. The iterative generation of a coherent structure with inherent fractal organization is assumed to control and to trigger the signal flux in the network. A model for fractal organization is derived from the modified Apollonian gasket shown in Fig. 2B. In this model the vectors u_i for construction of the tiles direct the flow of control signals i(u_i,t) setting up a polygonal or circular shaped array in a neurophysiological substrate under coherence as shown in Fig. 4. In Fig. 4C, I(t) stands for the ion flux for the time t through an ion channel in the center of one polygonal tile. The system flux I(t) is perpendicular to the control currents i(u_i,t) which modulate the opening of the ion channel protein. They propagate along the membrane and induce coherence in an array of membrane lipids surrounding the ion channel. The conformation of the channel protein and that of the surrounding membrane lipids is linked to each other in a complex manner since the majority of lipids constituting the nerve cell membrane is negatively charged and may react sensitively to alterations in Na/K-ion fluxes. Integration of ion fluxes in the nerve cell membrane is consistent with currently developed models for signal integration in the dendritic trunks or the cell bodies of nerve cells (Hoppensteadt F.C., 1989; Koch C., 1997; Orpwood, R.D., 1994; Segev I., 1998; Sporns et al., 1989). Fig. 4 C and D illustrate how this principle may be realized in the nerve cell membrane or in a putative "conscious bio-electronic chip". The system current I(t) conducted through the coherent space area with the size A is determined by the control currents i(u_i,t) depending on the directional vectors u_i (see Fig. 2B) according to:

I(t) = f(A,t) = f[sum of i(u_i,t) × i(u_i+1,t)] =

f[sum of i(u_i,t) i(u_i+1,t) sin [i(u_i,t),i(u_i+1,t)]]; Eq. 8

with u_i;u_i+1 = construction vectors of coherent space with a common angle as in Fig. 2B.

The system current I(t) can be correlated with the self by the assumption that I(t) is a function of f{S and X}. The function f{S and X} is then interpreted as a product vector perpendicular on u_i, a model already introduced for the construction of a three-dimensional space perceived in consciousness as described in Fig. 2D. Thereby, the self would be composed of a vector field generated by elementary and coherent tiles of a fractal structure and distributed throughout the brain. In the present model, the distribution would be triggered by the development of the system current I(t) which is relying on the conductance or resistence properties of the coherent area. These properties may be different for a fractally compared to a non-fractally structurized space. Since an intermediate decoherence would enter an iterative Markov process of downscaling, the coherent area may be trapped in a transfinite state between superposition of logical states by coherence and their particular manifestation on spatially distinct energy nodes. Iterative reverberation will proceed until eventually sufficient energy loss induces the final decay of the coherent state. If the system current is feedback-coupled to the control currents, there will be a characteristic oscillation frequence or resonance for I(t) distinguishing the fractal from the non-fractal behavior of the coherent area. It is assumed that there are specific resonance attractors (or repellors) reacting to harmonic frequency bands. An experimental verification of these assumptions is expected from the application of the patch-clamp technique to a nerve cell membrane triggered with control currents from different directions. A certain area of the membrane can be excised from the nerve cell by the tip of a micropipette. It will be enclosed by a polygonal or circular shaped mesh which is spiked by radial electrodes as shown in Fig. 2B. Fractal behavior can be analyzed by recording the oscillation characteristics of the action potentials upon tiggering the patch-clamped membrane with control currents generated between the surrounding electrodes. A direct structural analysis can be achieved by atomic force microscopy with the patch-clamped membrane spread on a mechanical support (Lärmer J. et al., 1997). Recent studies on nerve cell action potentials have shown a strict fractal dependence of the frequency to the power (amplitude) of the potential signals (Lowen S.B. et al., 1997). This can be explained by fractal thermal noise or fractally organized changes in the conformation of ion channel proteins reported previously (Liebovitch L.S. and Toth T.I., 1990). Another mechanism evoking the characteristics observed may be the fractal structurization of the nerve cell membrane. At any time the overall intensity of the potential would depend on the area size of the "elementary fractals" and the probability for signal release on their abundance in an extended fractal lattice. According to a model introduced Beck and Eccles the self is created by a quantum physical process deciding on the probability of a synaptosomal vesicle to merge with the nerve cell membrane in order to release its neurotransmitter content (Beck F. and Eccles J.C., 1992). A combination with a fractal lattice imprinted in the synaptic membrane would enable to control this process by coherence or decoherence of the elementary tiles. In this case signal flow along the membrane, fractal onset in the membrane bilayer and transmitter release would create a unified computational process for generation of the self in the human brain.

Conclusions and Perspectives

A model for a simultaneous realization of two distinct logical states by an undivided self was taken as a first entry to an explanation of perception in human consciousness. In the present approach the self as the perceiving entity emerges from the distribution of the information perceived to a fractally structurized space in the nerve cell membrane. Each different model at least has to cope with a self behaving like a "pseudoparticular" singularity and yet consciously experiencing a space filled with distinct objects. Previous approaches favor the idea that the self emerges from an operation termed "the holographic paradigm" which is developed from a model of holographic memory storage based on the convolution theorem and introduced by Dennis Gabor about thirty years ago (Gabor D., 1968; Jibu M. et al., 1994; Psaltis D. et al., 1990). This model describes the holographic superposition of information in form of spatially spread wave-functions. Spatial spreading, however, abandons the locality of logical states and in turn undoes the prerequisite for their distinction. When a hologram is imprinted on a grating support then the diffraction pattern is again a distribution of spatially distinct states. In this case, however, the holographic imprint will also face the problem of splitting the integrity of the self.

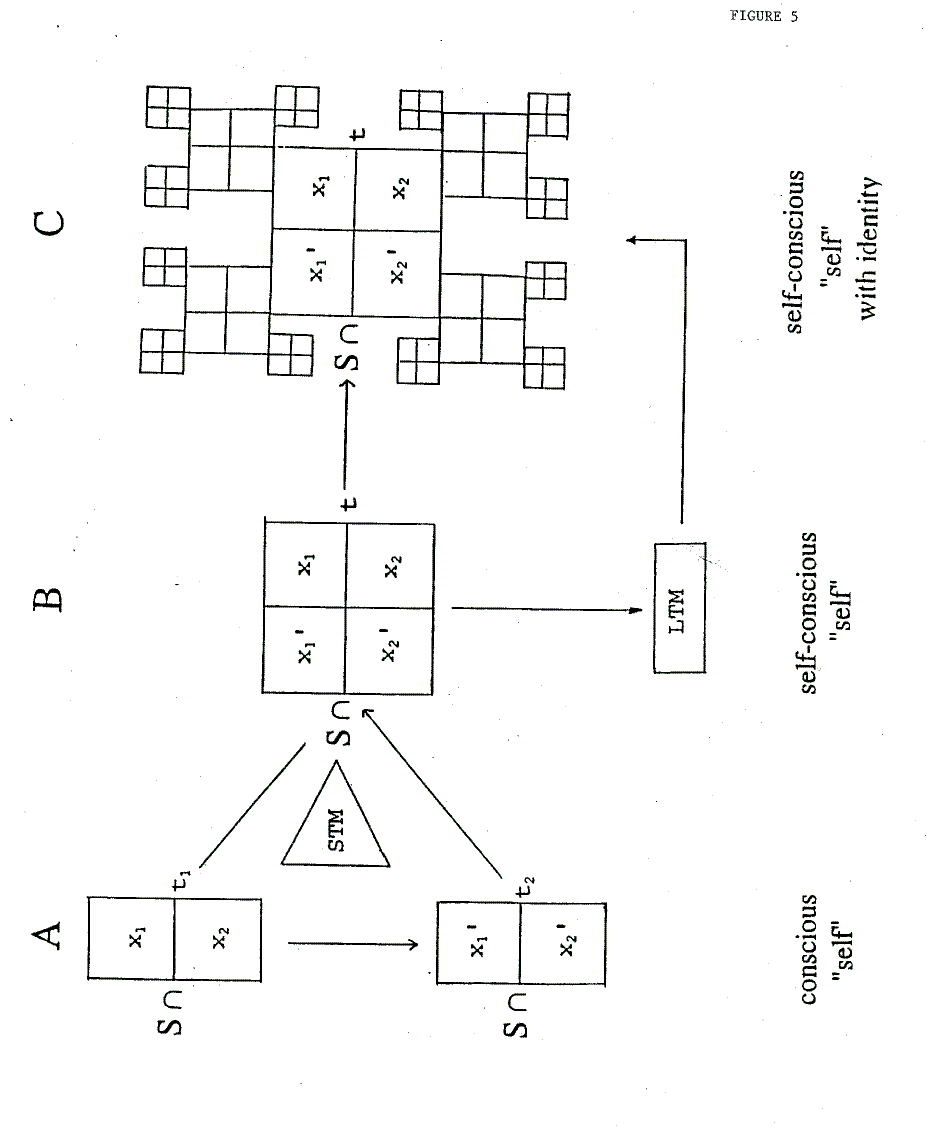
In a consequent application of a materialistic view it is inevitable that the self is not an independent entity but a quality inevitably arising from the proper arrangement of physical processes. That is to say clearly: the self has always been an immanent property of nature but has to become conscious just by an appropriately organized physical set-up. According to a thesis introduced by Liberman it is even possible to go further: each physical process with energy transformation is accompanied by an emotional quality if the generation of a self provides a conscious "inner point of view" (Liberman E.A. et al., 1989). A particular organization of our brain generates not only a self acting as an observer of objects, but is also observing itself, it is self-conscious. According to the present model this requires the inclusion of additional information in a fractal structure since the mere perception of physical objects does not inevitably entail that the perceiving entity is aware of its own existence. Fig. 5 illustrates a model describing the development of self-consciousness from a conscious self. The self related to the space perceived in consciousness evolves in time from {S and X(t₁)} to {S and X(t₂)}. The evolution of {S and X} is driven by a computation within the coherent state, and eventually is distributed by the collapsing fractal. The awareness of the self as continuity emerges from a confrontation of the present {S and X(t₂)} with the past {S and X(t₁)} in a common fractal "space-time" which is the benefit of having a memory. The mechanisms of this process are too elusive as to be an additional part of the present discussion but are likely to involve a superposition of stored nerve signals consistent with the "holographic paradigm" (Gabor D., 1968; Jibu M. et al., 1994; Psaltis D. et al., 1990; Stamenow M.I., 1996).

The self may develop in time by iteration of finite "time singularities" (similar to the those of spatial distribution) without losing its temporal integrity. It should be noted that just this integrity warrants the experience of sensations evolving in time like the beauty felt by listening to music. The continuous experience of one-self, however, does not necessarily entail a feeling of being a unique identity. Birds may have a continuous impression of their singing but one would doubt that they define themselves as personalities. In order to build up this identity the self must be fed with a big deal of one's memory in each moment of its existence. Only this simultaneous integration of past and present information ensures that we wake up in the morning as the same person we used to be when we fell asleep the night before. As shown in Fig. 5D this information maybe included within consciousness by a multi-fractal structure. It is possible that a self-conscious self with a feeling of its own identity is the precious gift only man awarded from nature. This does not exclude that in earlier stages of evolution simpler forms of a self were realized. In this study the application of the fractal concept to the internal structurization of the nerve cell membrane suggests a way for experimental verification by patch-clamping technique. The construction of the respective computational element may even found the technical basis for the artificial creation of conscious events in a machine.

Acknowledgment: The author wishes to thank Dr. Robert K.Yu and Dr. Matthew Tranduc for fruitful discussions and critically reading the manuscript.

References

Baars, J. (1997) In the theatre of consciousness. Journal of Consciousness Studies 4, 292-309.

Beck, F. and Eccles, J.C. (1992) Quantum aspects of brain activity and the role of consciousness. Proceedings of the Natlional Academy of Science USA 89, 11357-11361.

Becker, K. and Rahmann, H. (1995) Influence of ambient temperature on content and composition of brain gangliosides in vertebrates. Comp. Biochem. Physiol. B. Biochem. Mol. Biol. 111, 299-310.

Bieberich, E. (1998) The paradox of the computational mind, submitted.

Fröhlich, H. (1968) Long-range coherence and energy storage in biological systems. International Journal of Quantum Chemistry 2, 641-649.

Gabor, D. (1968) Improved holographic model of temporal recall. Nature 217, 1288-1289.

Gershenfeld, N.A. and Chuang, I.L. (1997) Bulk spin-resonance quantum computation. Science 275, 350-356.

Hoppensteadt, F.C. (1989) Intermittent chaos, self-organization and learning from synchronous synaptic activity. Proceedings of the National Academy of Science USA 86, 2991-2995.

Jibu, M., Hagan, S., Hameroff, S.R., Pribram, K.H. and Yasue, K. (1994) Quantum optical coherence in cytoskeletal microtubules: implication for brain function. Biosystems 32, 195-209.

Koch, C. (1997) Computation and the single neuron. Nature 385, 207-210.

Koh, D.S., Jonas, P. and Vogel, W. (1994) Na(+)-activated K+ channels localized in the nodal region of myelinated axons of Xenopus. Journal of Physiology (London) 479 (Pt 2), 183-197.

Lärmer, J., Schneider, S.W., Danker, T., Schwab, A. and Oberleithner, H. (1997) Imaging excised apical plasma membranes of MDCK cells in physiological conditions with atomic force microscopy. Pflüger's Archive-European Journal of Physiology 434, 254-260.

Liberman, E.A., Minina, S.V. and Shklovsky-Kordi, N.E. (1989) Quantum molecular computer model of the neuron and a pathway to the union of sciences. Biosystems 22, 135-154.

Liebovitch, L.S. and Toth, T.I. (1990) Using fractals to understand the opening and closing of ion channels. Annals of Biomedical Engineering 18, 177-194.

Lowen, S.B., Cash, S.S., Poo, M.-m. and Teich, M.C. (1997) Quantal neurotransmitter secretion rate exhibits fractal behavior. Journal of Neuroscience 17, 5666-5677.

Mandelbrot, B. (1982) The fractal geometry of nature. Freeman, San Francisco.

Monroe, C., Meekhof, D.M., King, B.E. and Wineland, D.J. (1996) A Schrödinger cat superposition state of an atom. Science 272, 1131-1136.

Orpwood, R.D. (1994) A possible neural mechanism underlying consciousness based on the pattern processing capabilities of pyramidal neurons in the cerebral cortex. Journal of Theoretical Biology 169, 403-418.

Peitgen, H.-O., Jürgens, H. and Saupe, D. (1992) Chaos and fractals, new frontiers in science. Springer Verlag, New York.

Pellionisz, A. and Llinas, R. (1980) Theoretical approach to the geometry of brain function: cerebellum coordination via a metric tensor. Neuroscience 5, 1125-1136

Penrose, R. (1994) Shadows of the mind. Oxford University Press Inc., New York.

Perillo, M.A., Scarsdale, N.J., Yu, R.K. and Maggio, B. (1994) Modulation by gangliosides of the lamellar-inverted micelle (hexagonal II) phase transition in mixtures containing phosphatidylethanolamine and dioleoylglycerol. Proceedings of the National Academy of Science USA 91, 10019-10023.

Psaltis, D., Brady, D., Gu, X.-G. and Lin, S. (1990) Holography in artificial neural networks. Nature 343, 325-330.

Segev, I. (1998) Sound grounds for computing dendrites. Nature 393, 207-208

Sperotto, M.M. and Mouritsen, O.G. (1991) Monte Carlo simulation studies of lipid order parameter profiles near integral membrane proteins. Biophysical Journal 59, 261-270.

Sporns, O., Gally, J.A., Reeke, G.N.Jr. and Edelman, G.M. (1989) Reentrant signaling among stimulated neuronal groups leads to coherency in their oscillatory activity. Proceedings of the National Academy of Science USA 86, 7265-7269.

Stamenow, M.I. (1996) The fractal-like roots of mind: a tutorial in direct access in Fractals of brain, fractals of mind (Cormac, E.M. and Stamenow, M.I., eds.). Advances in Consciousness Research 7, 273-322.

Strawson, G. (1997) The self. Journal of Consciousness Studies 4, 405-428.

Legends to the Figures

Figure 1:

Algebra of sets in human consciousness

Euler-Venn diagram for the description of products formed by the an irreducible "self" with spatially disjoint subsets A and nonA. Two paradoxical situations arise from a distributive intersection of S with A or nonA: Solution 1: S is split into two complementary subsets S(A) and S(nonA) and in turn unequals itself. Solution 2: The integrity of S is preserved but A and nonA are no longer complementary to each other and in turn cannot be distinguished by S. The ability of simultaneous perception of A and nonA by an undivided S is illustrated by solution "?".

Figure 2

Fractals in neural networks

A fractal downscaling according to the Sierpinski triangle can proceed by tiling (A) or dendritic networking (C). The two downscaling pathways merge to the same coherent structure with a fractal imprint indicated by a hexagonal tiling according to a modification of the Apollonian gasket (B). This can be interpreted as a model for a fractal distribution of wave-nodes for spatially spread energy states. The vectors given for the construction of each structure are subject to linear transformation as described in a general notation by determinant matrices in the equations underneath. The matrix coefficients describe a transformation of P_i(x_i,y_i) to P_i'(x_i',y_i') thereby generating a vector v_i. The operations for (A) and (C) are equivalent using a notation derived from either cartesian or polar coordinates. The matrix for polar coordinates is based on the assumption that there is first a rotation by followed by a translation. Iterative downscaling is achieved by the Hutchinson operator w. In (C) the contraction after rotation is obtained by the scaling factor r. The spatial adjustment of the v- and u-vectors is reached by elimination of the non-diagonal matrix coefficients in (B). Under coherence a different coordinate system with three principle axis x_i is used. This system forms the basis for the definition of points perceived in the space of consciousness (D). The self is either aware of one point in a three dimensional space (eye in the lower half) or of three points in a two-dimensional space (eye in the upper half). Depending on the spatial limit for coherence in each fractal, the distinct distribution of points forms a hyper-plane (e.g., P_a-P_c) which is experienced as a three-dimensional structure in the human mind.

Figure 3:

Signal flow in the brain

The divergent or convergent flow of nerve signals is described by direction vectors for each level of neuronal structures. Level 1, retina projection of the outer space; level 2, operational brain centers; level 3, neuronal network; level 4, generation of a fractal structure in a nerve cell (Apollonian gasket formed by patches of membrane proteins and surrounding lipids); level 5, space and objects perceived by the mind.

Figure 4:

Creation of fractal coherence

Biological, electronic, and hybrid elements for the generation of microscopic fractals. Control currents i_i are superimposed to a coherent distribution of oscillation nodes. Iterative decoherence and reverberation to the fractal determines the resonance frequency of the system current I. This process is suggested to generate conscious experience. A: "Classical" transistor; B: hybrid element, patch clamped nerve cell membrane with surrounding electrode spikes; C: nerve cell, Apollonian gasket as fractal in the membrane; D: electronic element (field effect transistor) for generation of a fractal (Sierpinski triangle); E-F: three elements combined to clusters with reentry of I directing i_i.

Figure 5:

Different levels of the self

In A spatial information is perceived by one-self but temporal connection is only given in B. In C the actual information from sensual organs is integrated with memory and provides the feeling of being a unique identity. STM = short term memory; LTM = long term memory.

end