home > Non-Standard Computation > Nanotechnology and complexity

StudyWebNotes and slides for a talk I gave on complexity and nanotechnology at the University of Aston's Computing for the New Millennium schools day, in January 1996. The audience were mainly 15-16 year old school children, interested in science. The aim of the day was to excite them about various whizzy science and technology they may not have come across in their schools courses. (Other talks included virtual reality and cryptography.)

As well as slides, I ran some demonstrations [which I can describe only briefly here] on an Acorn A4 computer.

Nanotechnology and complexity: consequences for computing

Abstract

Nanotechnology promises to deliver unparalleled benefits, but all these benefits require sophisticated and subtle programming of the nano-machines themselves. A swarm of benevolent nanites could increase our quality of life immensely; a swarm of rogue nanites could spell disaster. What computing paradigms are needed in order to help us gain the benefits while eliminating the risks?

Studies in Artificial Life, investigating properties of complex systems and emergent behaviour, help us understand how many small systems can combine to form a large system with qualitatively different behaviour. This understanding may pave the way to safe and robust programming of nanites.

This talk explores and discusses these various issues.

Nanomachines

Natural size scales

We tend to think that "more complex" goes with "bigger"

Technology size scales

Our technology is decreasing in size, yet getting more complex

Nano manufacturing

Nano machines manipulate matter at the molecular and atomic level.

A cow is a machine for turning grass, water and air into beef. A nanite could be designed to do the same thing directly. Pour grass into a hopper, fill the tank with water, switch on the power, and let the nanites get to work. A while later, open the door, and there's a steak!

In fact, nanites could in principle be designed to build just about anything that can be build by manipulating matter.

But how can a sub-microscopic machine build anything as large as a decent steak? It is is feasible because one of the things nanites could be designed to build is themselves -- they could be made self-replicating. So it is very easy to get enough nanites to build macroscopic objects.

Self-replication

Can we ever get enough nanites to build something macroscopic? What are self-replication timescales? We can make some very rough estimates, using 210 ~ 103, so every 10 doublings, we would have a 1000 times as many nanites

Ordinary cells can divide every 10 hours, embryonic cells every 10 minutes. So let's take a doubling time of 100 seconds (well over a minute). If at t=0 we had one nanite consisting of 1000 atoms, massing 10-23 kg then, if enough raw material were available:

Nano applications

Pollution control

And it's not just building new things. Nanites can rearrange what is already around. One quite exciting possibility is pollution control

Medical applications

As well as repairing the environment, eventually there might be nanites that could repair you.

Nano problems

Of course, all great advances come with associated problems. Before we get all these advantages from nanotechnology, we have to think about how we might solve these.

Nano viruses

One thing I mentioned is putting nanites in people, to help cure them of diseases. But what if the nanites go wrong? They might cause diseases.

Grey goo

The worst case scenario is known as the "grey goo" problem. Rogue nanites might get loose and disassemble the world, reducing it to grey goo.

Remember, we calculated that it took less than 5 hours for our self-replicating nanites to become a mass the size of the earth (given sufficient raw materials, of course...).

Safety critical programming

We will have to think about how we can program these nanites safely, so that they won't go wrong.

You have probably all heard about some software disaster or other, where something has gone horribly wrong. We are only just beginning to understand the problems of writing large software.

Programming nanites could make other exercises in safety critical programming look quite straightforward by comparison.

Programming nanites

And there are new kinds of problems if we want to program nanites.

The answers to these puzzles may lie in the new science of chaos, complexity, and self-organising systems.

A classical view of science

First, a classical view of science:

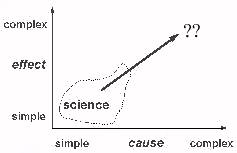
There are causes, that range from simple to complex, and there are effects, that also range from simple to complex.

The classical view is that simple causes result in simple effects, and complex causes give complex effects. In this view the world falls along this diagonal line.

Science tries to find simple causes and underlying laws, so this seems to necessarily mean it explains simple effects.

Depending how far up this line you go, the particular branch of science has different names : physics at the bottom, then chemistry, then biology.

And right at the top, we have things just too difficult for us at the moment.

Classical dynamics: attractors

So the classical view says we have simple equations giving simple behaviour.

For example, a + w x = 0 -- Simple Harmonic Motion: the equation describes the motion of a simple pendulum. The equation says that the restoring force is proportional to the displacement.

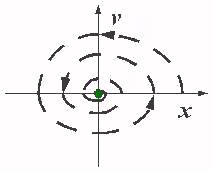
The graph is a plot of position against velocity. When the displacement is a maximum, the speed is zero. When the speed is a maximum, the displacement is zero.

In the real world there is always friction

a + k v + w x = 0 -- Damped Simple Harmonic Motion

This is the equation for a damped pendulum, where the damping is proportional to the speed. The maximum speed and maximum displacement get smaller on each swing.

So if we plot this damped motion, it spirals down to the centre: no speed, no displacement: it has stopped.

This is the classical view: simple equations describe simple behaviour.

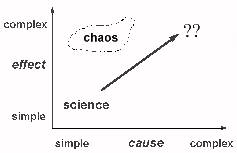Chaos

But the results of the new chaos science show us that this classical intuition is just false. Simple causes can have profoundly complex behaviours.

Coupled pendulums

[Here I demonstrated an 'executive toy', consisting of a pair of coupled pendulums containing small magnets, which exhibits fascinating chaotic behaviour.]

One reason why this science is so new is that it relies heavily on computers to explore the complex behaviour of simple equations. One might cynically think that the reason why it was thought simple equations have simple behaviours is that scientists only investigated equations they could solve by hand, which necessarily had simple solutions!

Logistic mapping

xn+1 = lambda xn (1-xn)

Let's plot the xn as a function of lambda.

[Here I ran a numerical simulation, which allowed the solution to build up slowly with increasing lambda, and talked through the features as they appeared.]

For small lambda, we do get equilibrium. Larger lambda, we get a bifurcation, or a period doubling. One year there is a big population, then a small one, then a big one. 'Boom and bust' cycles. As lambda continues to grow, we get more doublings. Eventually, we hit a chaotic region -- there is no equilibrium, and the behaviour appears random. But in this sea of chaos, there are strange islands of stability. There is a cycle with period 3: a region of predictability in a sea of chaos.

So if you see a behaviour that has boom and bust cycles, or appears not to be in equilibrium, there aren't necessarily peculiar or sinister forces causing it. It might just be the natural behaviour implicit in a very simple equation!

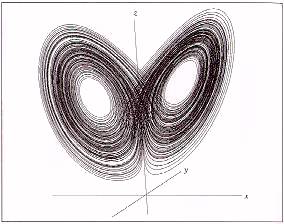Lorenz strange attractor

vx = 10 x - 10 y
vy = 28 x - y - x z
vz = x y - 8 z / 3

Here is a slightly more complicated set of equations. The speed in the x, y and z directions is given here. What sort of behaviour does this describe?

[I ran a numerical simulation of the Lorenz equations, allowing the solution to build up slowly. I talked through the features as they appeared.]

The initial behaviour looks like a transient. We seem to be in a nice cyclic place here. But wait! it's off somewhere. Now it's back. 3 times round this loop, then twice round the other...

So, there are times when the behaviour is periodic and predictable, as it cycles round one loop. And there are times when it flips to the other cycle. And even times when it appears random.

These equations are a very simplified and cut-down versions of a simple model of a weather system. So now you know why the weather may be so difficult to predict -- it is a chaotic system.

The shape of this path is a fractal. There is a deep connection between chaos and fractals.

Chaotic nanites

Nanites necessarily have small programs in them. And as we have see, even such a small program could have incredibly bizarre behaviour.

But not every small program is chaotic. So why am I making all this fuss? Isn't the answer just to choose those programs that aren't chaotic?

Because we may need to exploit that very chaos to get what we need: sufficiently complex behaviour. I will try to explain how ...

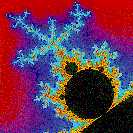Mandelbrot set

Let's look closer at fractals.

A fractal has the property of self-similarity. As you zoom in on its structure, yet more structure appears, which is similar (but not necessarily identical) to the higher level structure.

The Mandelbrot set is the classic example of a fractal. [I started a Mandelbrot set program, and zoomed in a few times.] The very simple generating equation, zn+1 := zn2 + c implicitly contains infinite levels of structure.

Fractals everywhere

But fractals occur in the real world, too: it's not just Mandelbrot sets!

Compression

With something like the Mandelbrot set, we have an enormously complex image encoded in a very small equation. So we can describe the image very simply. We say the image is compressed.

If we can go the other way -- start with a picture, find a fractal equation that produces it -- we can compress images. This is done routinely today -- many pictures you get on CD-ROMs use fractal image compression.

This might give us a clue about how DNA could hold enough information to describe creatures. Human DNA is about 3 billion bases. You could fit a complete description on a few CD-ROMs. There is software in existence of this sort of size -- but it certainly doesn't describe anything as complex as a person.

But we have seen that simple equations, simple algorithms, can describe very complex results. And if you look at a map of veins and arteries, for example, they look river-like, they look fractal. Maybe DNA contains a fractally compressed description?

Programming a nanite

So this might give us a clue about how we can fit a large task into a small program in a small nanite. We might need to use fractal algorithms.

This is still an open research area -- how to go from the behaviour we want to a compressed 'fractal algorithm' that encodes it.

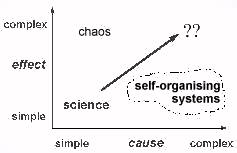Self-organisation

But this is only half the story. We want trillions of these nanites to cooperate to build macroscopic objects. Do we have any hope of controlling such a massively complex system?

There are indeed such things.

They are called self-organising systems, and they are everywhere, once you know where to look.

Boolean networks

Consider a network of light bulbs.

Each bulb is randomly wired to 2 others, which act as input signals. These inputs are fed through a random boolean function to say whether the bulb should be on or off. For example, the function might say the bulb is on only if both its inputs are on (the AND function), or if either is on (the OR function) or is on all the time. There are 16 possible such functions.

Start the network off with bulbs lit randomly. Each generation, determine the new state from its input state. The network has 2N possible different states, which for 400 bulbs is about a trillion different states. So you might imagine, given everything has been set up randomly, that the behaviour will look random, with bulbs flashing on and off in no discernible pattern. [Quick demo of 20x20 lights flashing at random.]

Let's watch what happens. [Demonstration of a Boolean network.] The pattern settles down very quickly, to a cycle length of very much less than N. This is truly astonishing! Totally unexpected behaviour. The very complex system has self-organised into a simple behaviour.

Aside: big numbers

Self-organising systems can involve huge numbers of separate components -- millions of billions, if not more, of cooperating entities. It is possible to visualise big numbers like these.

See this one litre carton here, it is 10cm on each side. Imagine marking off one side in millimetres -- so there's a hundred of them. Now imagine I've got a fine saw, and I saw along the marks, so the cube would be cut up into 100 sheets, 1mm thick, and 10cm square. Now mark millimeters along another edge. Imagine I saw it up again. Now I would have 100 squared, or 10,000, rods, 10cm tall, and 1mm thick. Now take the last side, and mark off millimeters, and I cut again. Now I would have got a load of 1mm cubes, 1 million of them! So you've just visualised a million.

Another way of seeing a million is to imagine this box filled up with grit or coarse sand, each grain about a millimetre across. There would be about a million grains of sand in here.

Imagine instead a 1 metre box, full of sand. That is a 1000 litres, so there are about a billion grains of sand there. So you have just visualised a billion. Imagine six of those boxes, and you have visualised a grain of sand for every person on the planet!

[See also Data Powers of Ten]

Emergent properties

Self-organising systems have emergent properties: something that is a property of the system as a whole, not of any of the individual components from which it is made. Emergent properties are simple properties of complex systems, and they are often surprising and unpredictable.

I'm going to show you how a system consisting of about a million components can have a simple property. [I slowly poured out my one million grains, or litre, of sand onto the table.] Notice how the slope of the sand pile stays roughly constant. If it is shallower than this critical slope, it waits for more sand to pile up. If it is steeper, avalanches occur. The system self-organises to a constant slope.

Other examples of self-organising systems:

At the "edge of chaos"

Many self-organising systems can be characterised by some parameter. When this parameter is too small, the system is static, frozen, fixed. When it is too large, the system is random, liquid, unstructured. But when it is just right, the system is in transition between these two stages. It has structures on all scales, and is "on the edge of chaos".

static complex random
physics solid phase-change liquid
Boolean nets sparse 2-way dense
biology non-life life death
economics totalitarian controlled laissez-faire
computing store compute process

The range of critical parameters is so very small, and you might think it would be hard to find and to maintain. But many self-organising systems seem to evolve themselves towards their critical parameter value. If they are too static, they loosen up a bit. If they are too fluid, they cool down a bit.

New perspective

For any complex system, including a system of nanites, to survive, it must be flexible. It must be flexible enough that it isn't frozen solid, but not so flexible that it is a random jumble.

What the study of complex self-organising systems is telling us is this. To be just flexible enough, a system has to have following properties:

If a complex system does not have these properties, we have a name for it: dead

Trillions of nanites

So our problem is how to organise trillions of nanites to cooperate to build some macroscopic object, without collapsing into random noise.

The study of self-organising systems offers us some hope in this area. Complex systems can have simple behaviours. What is more, they often spontaneously self-organise into these simple behaviours without any outside control. But the flexible, dynamic, evolving behaviour such a system must have doesn't yet fit in with the way we like to think about engineering software.

So the open question, that we don't yet have an answer to, is this: we know what property we want. How do we design a self-organising system that has this as an emergent property?

The future

So, to summarise: Nanotechnology offers fantastic rewards. But before we can reap those rewards, we have to solve at least two programming problems:

  1. Small programs for big tasks. How do we fit small programs into small nanites to perform complex tasks? Fractal algorithms may hold the key. But we don't yet have any science of fractal program compression
  2. Many nanites make light work. How do we get trillions of nanites to work together? Self-organising systems may be the route here. But we don't yet understand emergent properties, let alone how to design systems to exhibit some required emergent property.

And least you think this is all too science fictional to be taken seriously: these problems are not peculiar to nanotechnology. They have to be solved if we are going to develop truly versatile complex software for whatever purpose.

So these are the challenges. You here are the next generation of scientists and engineers. Maybe some of you will solve them.